Mathematics: Sextant angles

Vertical sextant angle · VSA

The triangle OBL can be described in terms of H, α and Distance,

$$\text{Distance}=\raisebox{1ex}{${\text{H}}_{}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{tan\; \alpha }}^{}$}\right.$$

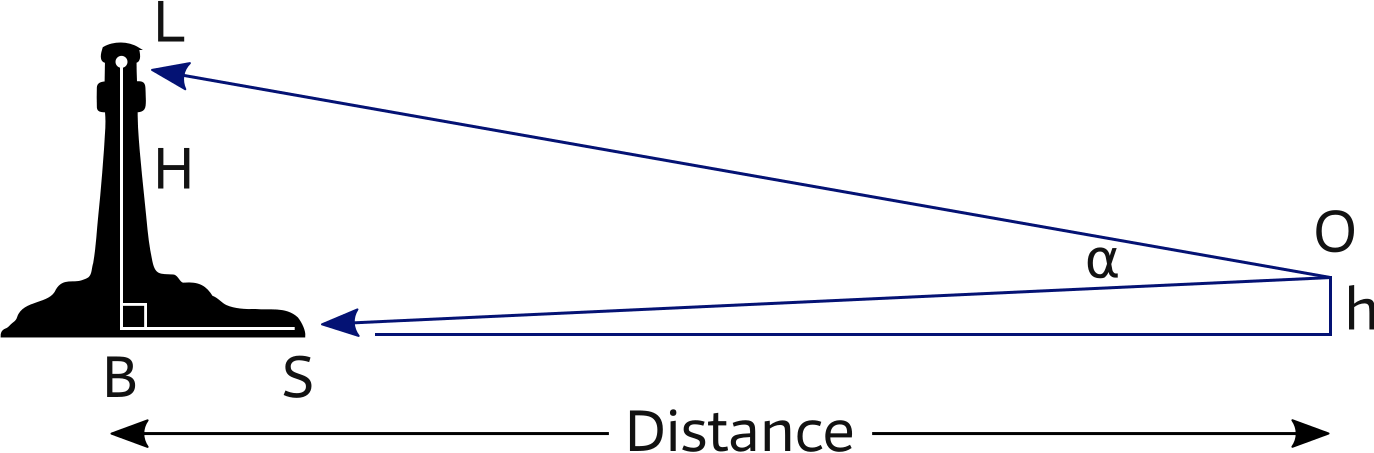
where the VSA vertical sextant angle α is in radians (see Chapter 5)radians (see Chapter 5) (0—2π) and both height and distance are in metres.

• Since 2π radians equals 360 degrees, the relations between radians and degrees are

$${\mathrm{Angle}}_{\mathrm{in\; degrees}}={\mathrm{Angle}}_{\mathrm{in\; radians}}\times \raisebox{1ex}{${\text{180°}}_{}$}\!\left/ \!\raisebox{-1ex}{${\text{π}}^{}$}\right.$$             and
$${\mathrm{Angle}}_{\mathrm{in\; radians}}={\mathrm{Angle}}_{\mathrm{in\; degrees}}\times \raisebox{1ex}{${\text{π}}_{}$}\!\left/ \!\raisebox{-1ex}{${\text{180 rad}}^{}$}\right.$$

• Since α is our VSA in radians, let's define
  A as the same angle in degrees, and
  a as the same angle in minutes total (i.e. arc minutes), $$\text{α}=\text{A}\times \raisebox{1ex}{${\text{π}}_{}$}\!\left/ \!\raisebox{-1ex}{${\text{180 rad}}^{}$}\right.$$
  and since A × 60 = a
  $$\text{α}=\frac{\mathrm{\pi }\times \mathrm{(a}/\mathrm{60)}}{\mathrm{180\; rad}}$$
  with π = 3.1416 we get $$\text{α}=\frac{\mathrm{a}}{3438}$$
• Since angle α is small we can use $$\tan \mathrm{(\alpha )}=\mathrm{\alpha }$$

$${\mathrm{Distance}}_{\mathrm{in\; metres}}=\text{H}\times \frac{{\text{3438}}_{}}{{\text{a}}^{}}$$

• Furthermore we favour nautical miles (NM) $${\mathrm{Distance}}_{\mathrm{in\; NM}}=\frac{\mathrm{Distanc}{\mathrm{e}}_{\mathrm{in\; metres}}}{1852}$$

Voilà, a very practical equation

It contains two notable approximations, both of neglitible influence. First, we left out the tangent function and second we used 3.1416 for π.

Realize that a smaller angle improves the approximation of omitting the tangent function. Yet, as an opposing effect the instrument error of a smaller sextant angle increases.

Intriguingly, the factor 1.856 is not a typo, and just by chance near to the nautical mile: 1.852 kilometres. If you are still reading, you are very brave person and might agree that it originates from

$$\text{1.856}=\frac{60\times 180}{\mathrm{\pi }\times 1852}$$

Eye height and tide

In practice no allowances are made for height of tide or height of eye; h in the figure above is usually ~2 m when seated in the cockpit. These factors are usually outside the precision of sextant measurements.
Futhermore, ignoring tide and h adds a small margin of safety since this will place the object (e.g. lighthouse) closer than it really is.

Distance lighthouse from cliff

So far we considered a perfect triangle (OBL), see figure, and forgot that life isn't always perfect, since the distance SB is sometimes too large to be ignored. This leads to an extra premise, which is seldom mentioned by other navigation textbooks:

the angle OLS should be ≥15°. 

Further reading

Without tides the Mediterranean is the perfect cruising venue with RYA & ASA sailing schools out of Athens into the Saronic or Cyclades (Santorini, Paros, Mykonos,…) and in the Ionian: Lefkas,
or back to chapter 5 of the navigation course,
or learn to sail bareboat with a private RYA ASA instructor.