Mathematics: Distance of horizon

Distance of horizon

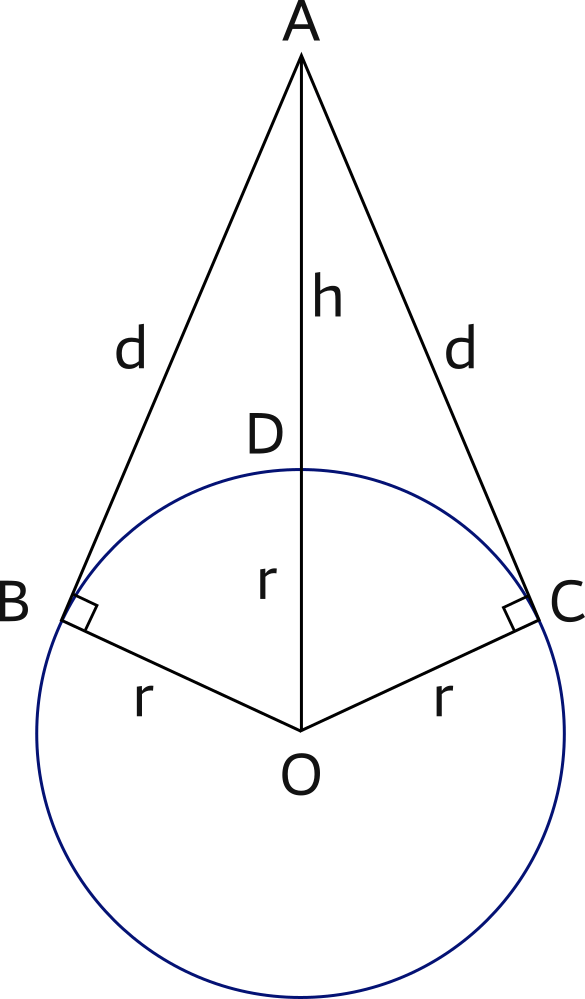
AD = h is the height of eye above the earth.
DO = BO = CO = r (radius of the earth).

Fact: any angle between a tangent line to a circle and the radius of the circle is a right angle.

Since we have a right triangle ABO where AB = d,
AO = h+r and BO = r,
we can find a formula for d in terms of h:
(AO)² = AB² + BO²
(h+r)² = d² + r²
d = sqrt[(h + r)² − r²)],
where r is approx. 3440.1 NM

An example: Let the eye height (h) be 4 meters (= 0.0022 NM); find the distance in NM of the geometrical horizon.
d = sqrt[(0.0022 + 3440.1)² − 3440.1²)]
d = sqrt[11834303 - 11834288]
d = sqrt[15.146]
d = 3.89 NM (geometrical)

The distance of the visible horizon as found in the table is greater (4.2 NM) due to atmospheric refraction.
The semi-empirical function used is:
d = sqrt[ (2 × 3440.1 × h) / (1852 × ρ_o) ], where ρ_o accounts for refraction (0.8279).

Next math chapter: Sextant angles,
or back to chapter 5 of the navigation course,
or learn to sail bareboat, skippered instruction or at RYA ASA sailing schools in Greece and beyond…