Mathematics: Distance of horizon

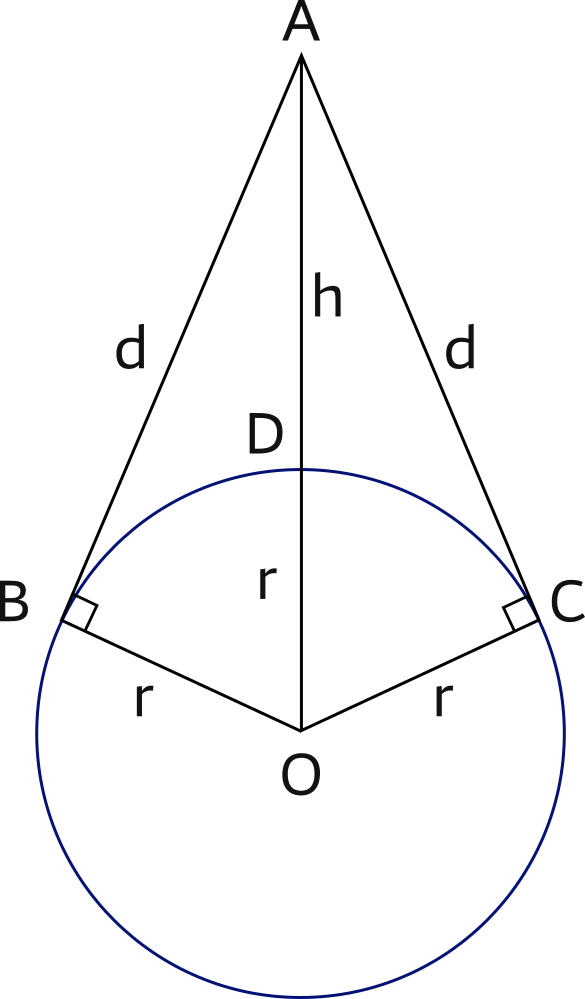
AD = h is the height of eye above the earth.
DO = BO = CO = r (radius of the earth).

Any angle between a tangent line to a circle and the radius of the circle is a right angle.

Since we have a right triangle ABO where AB = d,
AO = h+r and BO = r,
we can find a formula for d in terms of h:
$\mathbf{A}{\mathbf{O}}^{\mathbf{2}}\mathbf{=}\mathbf{A}{\mathbf{B}}^{\mathbf{2}}\mathbf{+}\mathbf{B}{\mathbf{O}}^{\mathbf{2}}$
$\mathbf{(}\mathbf{h}\mathbf{+}\mathbf{r}{\mathbf{)}}^{\mathbf{2}}\mathbf{=}{\mathbf{d}}^{\mathbf{2}}\mathbf{+}{\mathbf{r}}^{\mathbf{2}}$
$\mathbf{d}=\sqrt{{\left(\mathbf{h}+\mathbf{r}\right)}^2-{\mathbf{r}}^2}$
where r is approx. 3440.1 NM

Distance of horizon example

Let the eye height (h) be 4 metres = 0.0022 NM; find the distance in NM of the geometrical horizon.
$\mathbf{d}=\sqrt{{\left(\mathrm{0.0022}+\mathrm{3440.1}\right)}^2-{\mathrm{3440.1}}^2}$
$\mathbf{d}=\sqrt{11834303-11834288}$
$\mathbf{d}=\sqrt{15.146}$
d = 3.89 NM (geometrical)

The distance of the visible horizon as found tabulated (e.g. in nautical almanacs) is greater (4.2 NM) due to atmospheric refraction.
The semi-empirical function used is
$\mathbf{d}=\sqrt{\frac{2 \mathbf{\times } 3440.1 \mathbf{\times } \mathbf{h}}{1852 \mathbf{\times } {\mathbf{\rho }}_{\mathbf{0}}}}$
where ρ_o accounts for refraction (0.8279).

Next math chapter: Sextant angles,
or back to chapter 5 of the navigation course,
or learn to sail bareboat, skippered instruction or at RYA ASA sailing schools in Greece and beyond…