See the previous chapter…
- Course overview: goals and introduction
- Positions: latitude, longitude, nautical mile, scale, knots
- Nautical chart: coordinates, positions, courses, chart symbols, projections
- Compass: variation, deviation, true • magnetic • compass courses
- Plotting and piloting: LOPs, (running) fix, dead reckoning, leeway, CTS, CTW, COG
- Advanced piloting: double angle on the bow • four point • special angle fix, distance of horizon, dipping range, vertical sextant angle, radians, estimation of distances
- Astronomical origin of tides: diurnal, semi-diurnal, sysygy, spring, neap, axial tilt Earth, apsidal • nodal precession, declination Moon and Sun, elliptical orbits, lunar nodes
- Tides: tidal height prediction, chart datums, tidal curves, secondary ports
- Tidal streams and currents: diamonds, Course to Steer, Estimated Position
- Aids to navigation: buoys, leading lights, ranges, characteristics, visibility
- Lights and shapes: vessels sailing, anchoring, towing, fishing, NUC, RAM, dredging
6 – The astronomical origin of tides
A reliable rhythm
Tides are a regular and ubiquitous phenomenon for those living near the sea.
The rhythmic rising and falling of the sea level can be as small as 0.5 m at mid-ocean locations such as Hawaii, or as big as 14 – 15 m in narrow bays such as the Bay of Fundy in Canada, or at Chausey (pictured below) near Mont Saint Michel [Wiki] in France.
However, regardless of the amplitude of the tides, they all have the same period; at virtually all seaside locations, there are two high tides and two low tides every 24 hours and 50 minutes.

The Sound Channel, with the Grande Cale on the right that dries completely at low tide; Hi-res image
This extreme tide took place in 2015, during a minor lunar standstill.
In a more complete analysis, tides are generated by forces imposed on Earth that are caused by a combination of gravity and motion among Earth, the Sun, and the Moon. The latter body being the major cause of our tides.
Definition of tide
Tide – from the sailor's perspective – is the vertical rise and fall of the sea level surface caused primarily by the change in gravitational attraction, the tide raising forces or tidal effect, of the Moon and Sun.
In astronomy, the tidal force is defined as a gravitational effect that stretches a body due to a gradient (difference in strength) in the gravitational field from a second body. The gradient means that the nearest side is attracted more strongly than the farthest side, causing a body to get stretched.
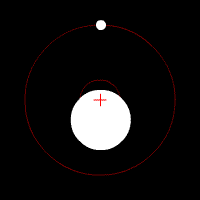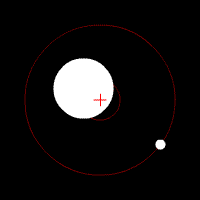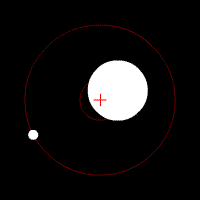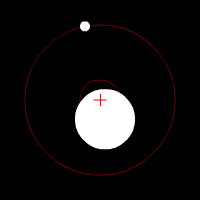
Earth and Moon orbiting around the barycenter (+), simplified with a circular orbit.
The Moon and the Earth are tethered together by gravity while rotating around a common center of mass called the barycenter – from Ancient Greek: βαρύς heavy + κέντρον center – which is the balance point of the system, located ±1600 kilometers beneath Earth’s surface, also providing the centripetal force necessary to maintain the orbiting motions, see Earth – Moon Barycenter [Youtube animation].
It is because the Earth’s mass is so much greater than that of the Moon that the barycenter isn't halfway in between the two bodies. The Earth's mass is ±6 × 1024 kg, whereas the Moon's mass is ±7.4 × 1022 kg. Therefore the Earth's mass is about 81 times greater.
Just as the balance of gravity and motion serve to keep bodies in stable mutual orbits without colliding, they also exert an influence on every particle of water on Earth, thus creating the tides.
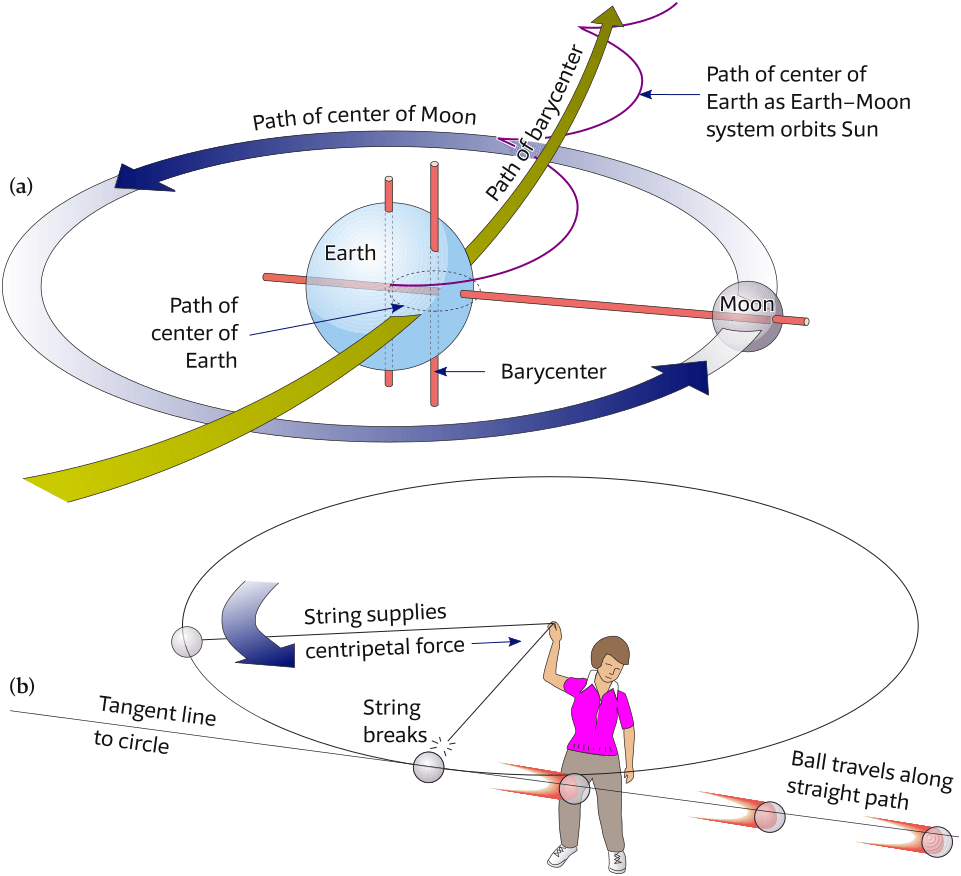
(a) The center of mass (barycenter) of the Earth – Moon system moves in a nearly circular orbit around the Sun.
(b) If a ball with a string attached is swung overhead, it stays in a circular orbit because the string exerts a centripetal (center-seeking) force on the ball. If the string breaks, the ball will fly off along a straight path along a tangent to the circle.
No floating off…
Just as the Moon experiences a gravitational pull from the Earth – which is why it orbits the Earth – so too the Earth experiences a pull from the Moon.
At the surface of the Earth, the pull from the Earth is much stronger than the pull from the Moon, for 2 reasons:
- the ocean is a lot closer to the Earth's center;
- the Earth has a far greater mass than the Moon.
Therefore, nor the ocean nor its seafarers will float off towards the Moon.
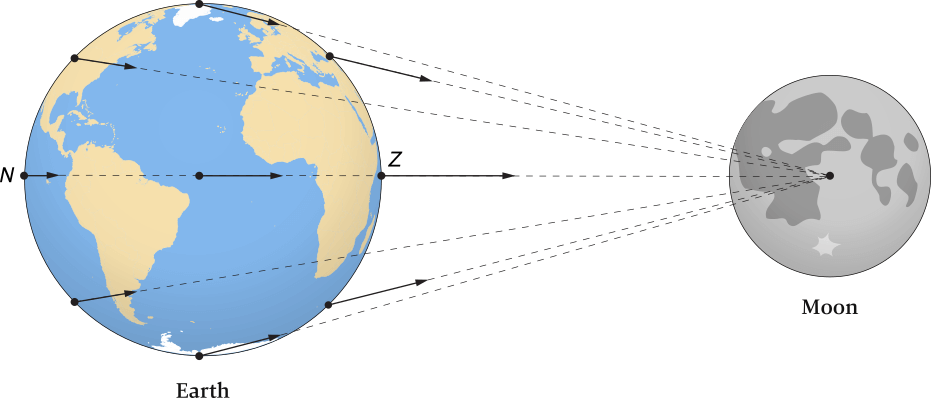
The gravitational forces on objects located at different places on Earth due to the Moon are shown by arrows. The length and orientation of the arrows indicate the strength and direction of the gravitational force. Notice the length and angular differences of the arrows for different points on Earth. The letter Z represents the zenith; N represents the nadir.
Distance between Earth and Moon not shown to scale.
Earth centered on the Atlantic for illustrative purposes.
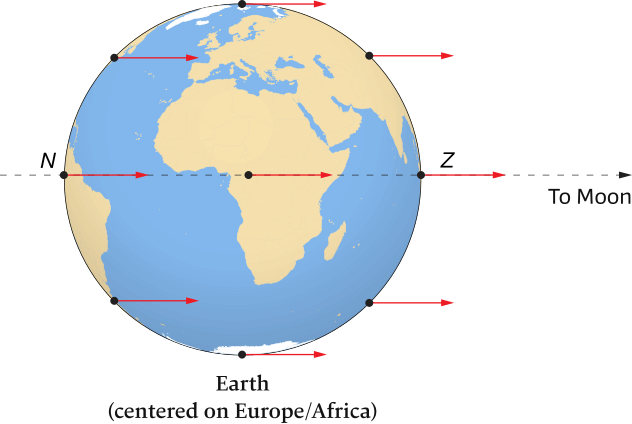
Centripetal forces required to keep identical-sized particles in identical-sized orbits as a result of the rotation of the Earth – Moon system around its barycenter.
Notice that the arrows are all the same length and are oriented in the same direction for all points on Earth.
It is a safe assumption that ancient mariners and those living near the coasts, see tidal history of the classical era [Wiki], will have tried to explain and forecast the tides.
Only around 330 BCE the Greek astronomer and explorer Pytheas [Wiki] discovered that the tides where somehow controlled by the Moon, according to the earliest written history of tidal theory [PDF].
However, it wasn’t until Isaac Newton (1642 – 1727) developed the universal law of gravitation that the tides could adequately be explained.

Origin of tides
Simplistically, it is the gravitational attraction of the Sun and Moon on Earth that creates ocean tides. In a more complete analysis, tides are generated by forces imposed on Earth that are caused by a combination of gravity and motion among Earth, the Moon, and the Sun.
Forces that produce tides
Newton’s work on quantifying the forces involved in the Earth – Moon – Sun system led to the first understanding of the underlying forces that keep bodies in orbit around each other. It is well known that gravity tethers the Sun, its planets, and their moons together.
For example, most of us are taught that “the Moon orbits Earth,” but it is not quite that simple. As shown in Figure 6.1, the two bodies actually rotate around a common center of mass called the barycenter, which is the balance point of the system, located 1600 kilometers beneath Earth’s surface. The wide green arrow in Figure 6.2 (a) shows the smooth, nearly circular path of the Earth – Moon barycenter around the Sun.
If the Moon and Earth and attracted to one another, why don’t the two collide? Moreover, the Earth – Moon system is involved in a mutual orbit held together by gravity and motion, which prevents the Moon and Earth from colliding. This is how orbits are established that keep objects at more or less fixed distances.
Newton’s work also allowed an understanding of why the tides behave as they do. Just as gravity and motion serve to keep bodies in mutual orbits, they also exert an influence on every particle of water on Earth, thus creating the tides.
Gravitational and centripetal forces in the Earth – Moon system
To understand how tide-generating forces influence the oceans, let’s examine how gravitational forces and centripetal forces affect objects on Earth within the Earth – Moon system.
(We’ll ignore the influence of the Sun for the moment.)
The gravitational force is derived from Newton’s law of universal gravitation, which states that every particle of mass in the universe attracts every other particle of mass. Stated mathematically, the attraction occurs with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between the masses. This can partly be expressed as
The inverse square law
The inverse square law [Wiki] stating e.g. that if two celestial bodies are 2 times as far away, the gravitational pull is 4 times less, or if 10 times farther away, the gravitational pull is 100 times less.
Gravitation:
Which means that gravity ∝ 1/distance2 – the symbol ∝ stands for “is proportional to” – so gravity is inversely proportional to the distance squared.
Applying this inverse square proportionality to the Earth's tides, there is a high tide on the side nearest the Moon because the Moon pulls the water away from the Earth, and a high tide on the opposite side because the Moon pulls the Earth away from the water on the far side.
Figure 6.5 demonstrates that the tidal influence on the closer sphere is greater.
This is due to the larger drop in gravitational force [Wiki], which gives a greater ratio of the force on the near side of the sphere to that on the far side.
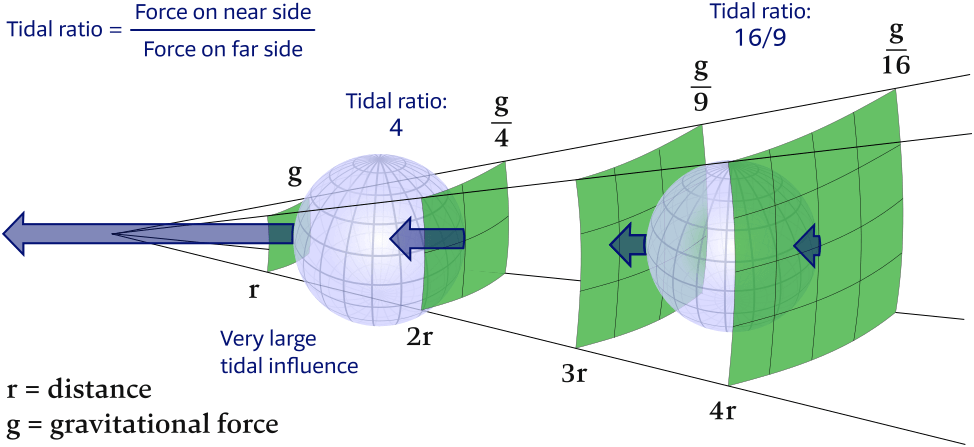
The tidal ratio of the force per unit mass on the near side compared to that on the far side
is much larger for the closer object. This is the reason that the Moon is the dominant tidal influence,
because the fractional difference in its force across the Earth is greater than
the fractional difference seen from the Sun. This difference in force follows the inverse square law.
If mass increases ( ), then gravitational force increases ( ).
An example of this can be seen in objects with a large mass (such as the Sun), which produces a large gravitational force. The rest of Newton’s law can be expressed as
If distance increases ( ), then gravitational force greatly decreases ( ).
The equations of Newton’s law show that gravitational attraction varies with the square of distance, so even a small increase in the distance between two objects significantly decreases the gravitational force between them. This is why astronauts experience weightlessness in space when they get far enough from Earth’s gravitational pull. In summary, then, the greater the mass of the objects and (especially) the closer they are together, the greater their gravitational attraction.
Figure 6.3 shows how gravitational forces for points on Earth (caused by the Moon) vary depending on their distances from the Moon. The greatest gravitational attraction (the longest arrow) is at Z, the zenith (zenith = a path over the head), which is the point closest to the Moon. The gravitational attraction is weakest at N, the nadir (nadir = opposite the zenith), which is the point farthest from the Moon. The direction of the gravitational attraction between most particles and the center of the Moon is at an angle relative to a line connecting the center of Earth and the Moon, see Figure 6.3. This angle causes the force of gravitational attraction between each particle and the Moon to be slightly different.
The centripetal force required to keep planets in their orbits is provided by the gravitational attraction between each of them and the Sun.
Centrifugal vs centripetal
In the rotating systems of Earth, Moon and Sun, it is the reference of frame that decides whether it more suitable to deploy a centrifugal force (“fugare” is latin for “to flee”) or a centripetal force (“petere” is latin for “to seek”, “to pursue”).
See centrifugal and centripetal.
A centripetal force “tethers” an orbiting body to its parent, pulling the object inward toward the parent, “seeking the center” of its orbit.
For example, if you tie a string to a ball and swing the tethered ball around your head, Figure 6.2 (a), the string pulls the ball toward your hand. The string exerts a centripetal force on the ball, forcing the ball to seek the center of its orbit. If the string should break, the force is gone and the ball can no longer maintain its circular orbit.
The ball then flies off in a straight line, tangent to the circle, Figure 6.2 (b), “tangent” meaning: a straight line touching a curve at a single point without crossing it there – “linea tangens“ is Latin for “a touching line”.
The Earth and Moon are tethered, too, not by strings but by gravity.
Gravity provides the centripetal force that holds the Moon in its orbit around Earth. If all gravity in the solar system could be shut off, centripetal force would vanish, and the momentum of the celestial bodies would send them flying off into space along straight-line paths, tangent to their previous orbits.
Resultant forces
Particles of identical mass rotate in identical sized paths due to the Earth – Moon rotation system, see Figure 6.4. Each particle requires an identical centripetal force to maintain it in its circular path. Gravitational attraction between the particle and the Moon supplies the centripetal force, but the supplied force is different than the required force (because gravitational attraction varies with distance from the Moon) except at the center of Earth. This difference creates tiny resultant forces, which are the mathematical difference between the two sets of arrows shown in Figure 6.3 and Figure 6.4.
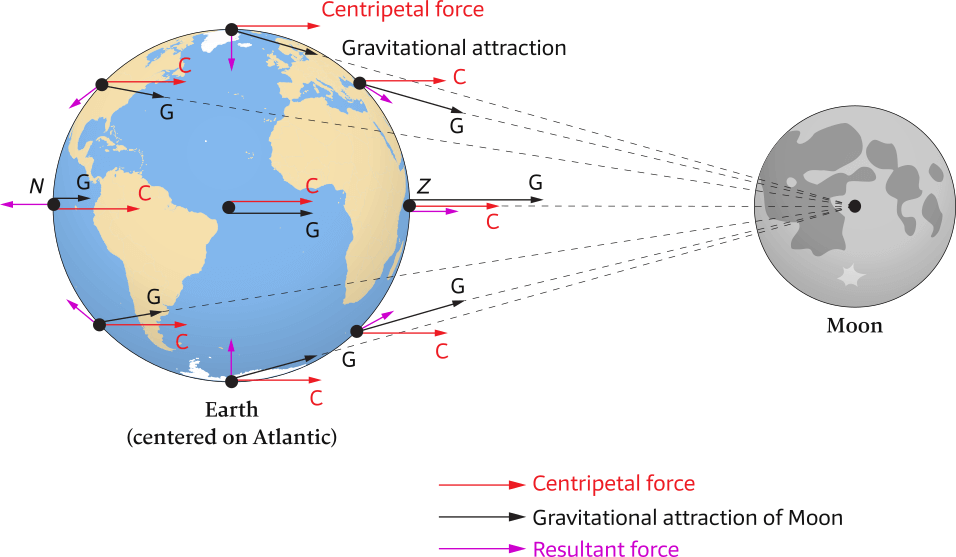
Red arrows indicate centripetal forces (C), which are not equal to the black arrows that indicate gravitational attraction (G).
The short purple arrows show resultant forces (or rather resulting deforming forces), which are established by constructing an arrow from the tip of the centripetal (red) arrow to the tip of the gravity (black) arrow and located where the red and black arrows begin.
The resulting deforming force deforms the Earth until it is in equilibrium with the elastic force (which therefore “wants” to make the Earth spherical again).
Distance between Earth and Moon not shown to scale.
Figure 6.6 combines Figures 6.3 and 6.4 to show that resultant forces are produced by the difference between the required centripetal (C) and supplied gravitational (G) forces.
However, do not think that both of these forces are being applied to the points, because (C) is a force that would be required to keep the particles in a perfectly circular path, while (G) is the force actually provided for this purpose by gravitational attraction between the particles and the Moon.
The resultant forces, or rather resultant deforming forces, (purple arrows) are established by constructing an arrow from the tip of the centripetal (red) arrow to the tip of the gravity (black) arrow and located where the red and black arrows begin.
Ultimately, the centripetal force is a sum of a component of the Moon's gravity and the elastic force that prevents further deformation (or breaking off parts) of the Earth.
Tide-generating forces
It is crucial to realize that the resultant forces demonstrated in Figure 6.6 are minute, averaging about one-millionth the magnitude of Earth’s gravity.
If the resultant force is vertical to the Earth’s surface, as it is at both the zenith and nadir (oriented upward) and along an “Equator” connecting all points halfway between the zenith and nadir (oriented downward), it has no tide-generating effect, see Figure 6.7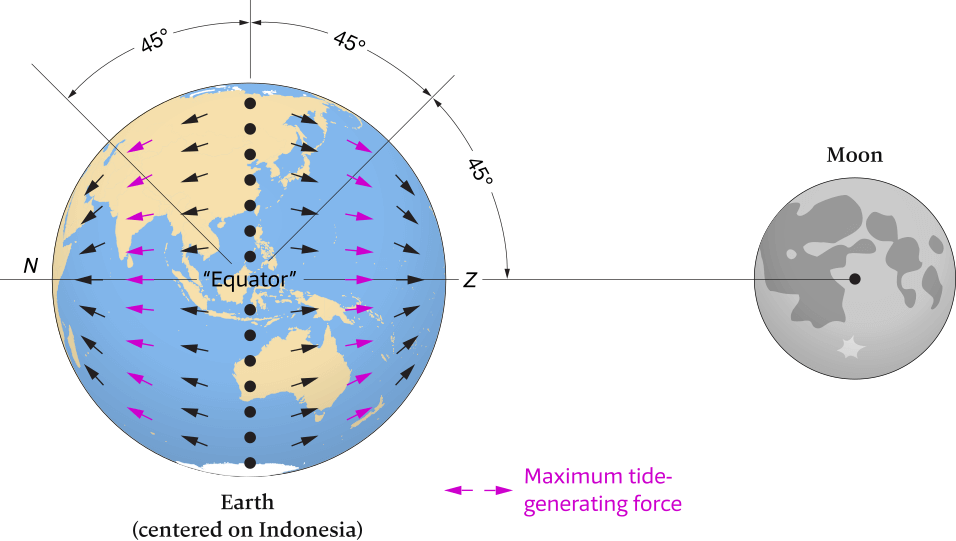
Where the resultant force acts vertically relative to Earth’s surface, the tide-generating force is zero. This occurs at the zenith (Z) and nadir (N), and along an “Equator” connecting all points halfway between the zenith and nadir (black dots).
However, where the resultant force has a significant horizontal component, it produces a tide-generating force on Earth. These tide-generating forces reach their maximum value at points on Earth’s surface at a “latitude” of 45 degrees (purple arrows) relative to the “Equator” mentioned here.
Distance between Earth and Moon not shown to scale.
However, if the resultant force has a significant horizontal component — that is, tangential to Earth’s surface — it produces tidal bulges on Earth, creating what are known as the tide-generating forces. These tide-generating forces are quite small but reach their maximum value at points on Earth’s surface at a “latitude” of 45 degrees relative to the “Equator” between the zenith and nadir, see Figure 6.7.
As previously discussed, gravitational attraction is inversely proportional to the square of the distance between two masses.
The tide-generating force, however, is inversely proportional to the cube of the distance between each point on
Earth and the center of the tide-generating body (Moon or Sun). Although the tide-generating force is derived from the gravitational force, it is not linearly proportional to it. As a result, distance is a more highly weighted variable for tide-generating forces.
The tide-generating forces push water into two bulges: one on the side of Earth directed toward the Moon (the zenith) and the other on the side directed away from the Moon (the nadir), see Figure 6.7.
The water flows horizontally, see Figure 6.8, following the green arrows – not fighting against the Earth's gravitational pull – literally being pulled by the Moon.
At the sub-lunar point (the zenith; the point where the Moon is directly above) and the nadir (opposite of the zenith aka the antipodal point) the water piles up and the sea level becomes slightly higher.
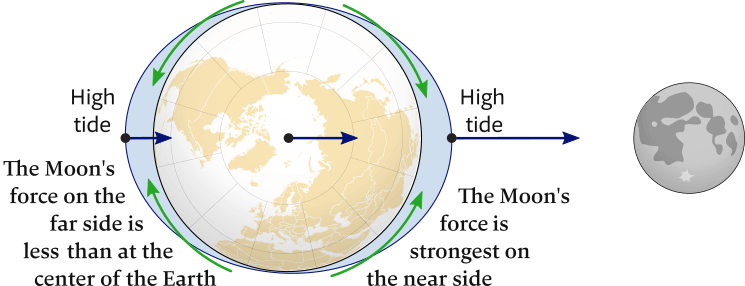
The Moon's gravitational field (navy blue arrows) on the near side is 1.068 × that on the far side, 6.8% differential accross the Earth
The green arrows show the directions of the water flowing along the Earth's surface towards the nadir and zenith.
The tidal bulges are greatly exaggerated, and in fact the sea level mid-ocean is only raised ±1 meter.
On the side directly facing the Moon, the bulge is created because the provided gravitational force is greater than the required centripetal force. Conversely, on the side facing away from the Moon, the bulge is created because the required centripetal force is greater than the provided gravitational force.
Although the forces are oriented in opposite directions on the two sides of Earth, the resultant forces are equal in magnitude, so the bulges are equal, too.
The tides are caused by an imbalance between the required centripetal and the provided gravitational forces acting on Earth.
This difference produces residual forces, the horizontal component of which pushes ocean water into two equal tidal bulges on opposite sides of Earth.
The Moon’s tidal effect
It is easier to understand how tides on Earth are created if we consider an ideal Earth and an ideal ocean.
The ideal Earth has two tidal bulges, one toward the Moon and one away from the Moon (called the lunar bulges), as shown in Figure 6.9.
The ideal ocean has a uniform depth, with no friction between the seawater and the sea floor.
In fact, Newton made these same simplifications when he first explained Earth’s tides.
Since the Earth rotates on its axis there is an equatorial bulge of both earth and water, but this is treated as a “baseline” shape against which tidal variations are referenced, a discussion of tides does not need to mention centrifugal forces. That only invites confusion and misconceptions.
Centrifugal forces are not tidal (tide-raising) forces. In a rotating coordinate system the centrifugal force of Moon on Earth is constant in size and direction over the volume of the Earth, therefore it has no tide associated with it.
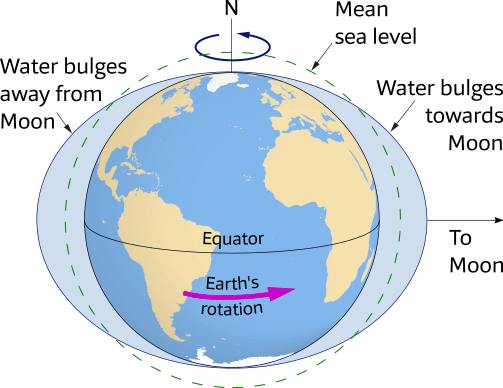
In an idealized case, the Moon creates two bulges in the ocean surface: one that extends towards the Moon and the other away from the Moon.
As Earth rotates, it carries various locations into and out of the two tidal bulges so that all points on its surface (except the poles) experience two high tides daily.
If the Moon is “stationary” and aligned with the ideal Earth’s equator, the maximum bulges will occur on the equator on opposite sides of Earth. If you were standing on the equator, you would experience two high tides each day. The time between high tides, which is the tidal period, would be 12 hours. If you moved to any latitude north or south of the equator, you would experience the same tidal period, but the high tides would be less high, because you would be at a lower point on the bulge.
In most places on Earth, however, high tides occur every 12 hours 25 minutes because tides depend on the tidal day (aka lunar day), not the solar day.
Synchronous rotation of the Moon
The Moon always shows the same face to the Earth –
not because the Moon doesn't rotate – but
because the Lunar Day is exactly equal to the Lunar Year (how long it takes to orbit the Earth).
In other words: the Moon rotates at the same rate as its orbital motion.
The condition where the year and day are equal is called synchronous rotation, and in the Moon's case it has been caused by the same tidal drag that moves the oceans and is slowing the Earth's rotation.
Tidal day
An earth day or solar day is a 24-hour period: the time it takes for the Earth to rotate 360° on its axis.
Yet, the Moon – which is in reality not “stationary” – also revolves during this 24-hour period around the Earth in the same direction: a prograde direction.
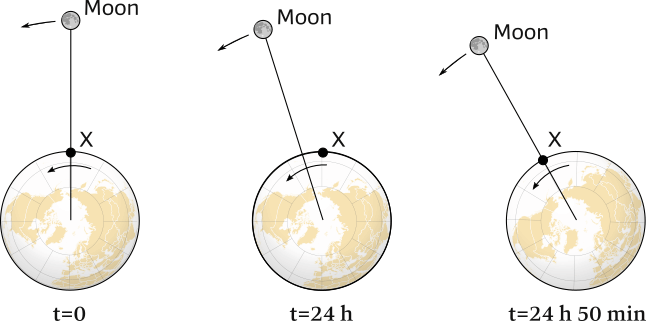
During the 24 hours that the Earth rotates from X at t=0 back to X at t=24 h,
the Moon will have travelled around the Earth as well.
And it takes a further 50 minutes to align X and the Moon again: t=24 h 50 min.
A tidal day (sometimes called tidal cycle or lunar day) takes longer: 24 hours and 50 minutes, which is why high tide is 50 minutes later and the Moon rises 50 minutes later the next day, see Figure 6.10.
Note that the term lunar day has several other meanings [Wiki],
hence the term tidal day is dominant.
The tidal day is measured from the time the Moon is on the meridian of an observer – i.e. directly overhead – to the next time the Moon is on that meridian and is 24 hours 50 minutes 28 seconds.
Similarly, the solar day is measured from the time the Sun is on the meridian of an observer to the next time the Sun is on that meridian and is 24 hours.
- Although a lunar day is equal to a tidal day with respect to tides, a lunar day has other definitions.
“Tidal day” is therefore the preferred term, but "tidal cycle" can also used. - A solar day (24 hours) is shorter than a tidal day (24 hours and 50 minutes). During one complete rotation of Earth (the 24-hour solar day), the Moon moves eastward 12.2 degrees, and Earth must rotate an additional 50 minutes for the Moon to be again on the meridian (directly overhead) of our observer
Tides are universal
The Moon and the Sun act on all nearby objects that have the ability to flow such as water in lakes or gasses in the atmosphere – and even deform the solid Earth.
In the ocean the height is just 1 meters, but that is large enough for water to move into the tidal bulges.
Smaller waters such as Lake Michigan can be raised about 5 cm. And even the water in a swimming pool experiences a tidal influence, although unmeaserable small.
In contrast, the tides in the atmosphere and the “solid” Earth have greater significance.
Tides in the atmosphere – called atmospheric tides – can be kilometers high.
The tides inside Earth’s interior – called solid-body or Earth tides – cause a slight but measurable stretching of Earth’s crust, typically only several centimeters high.
Tides are everywhere: e.g. further away in our solar system there is the tidal heating of Jupiter's Io moon [Wiki].
The Sun's tidal effect
The Earth orbits around the Sun – with one revolution in one year – creating a gravitational interaction, which yields two solar tidal bulges per day (24 hours), inherently semidiurnal, half daily (meaning twice per 24 hours), due to the Earth's 24 hour day (revolution on its own axis).
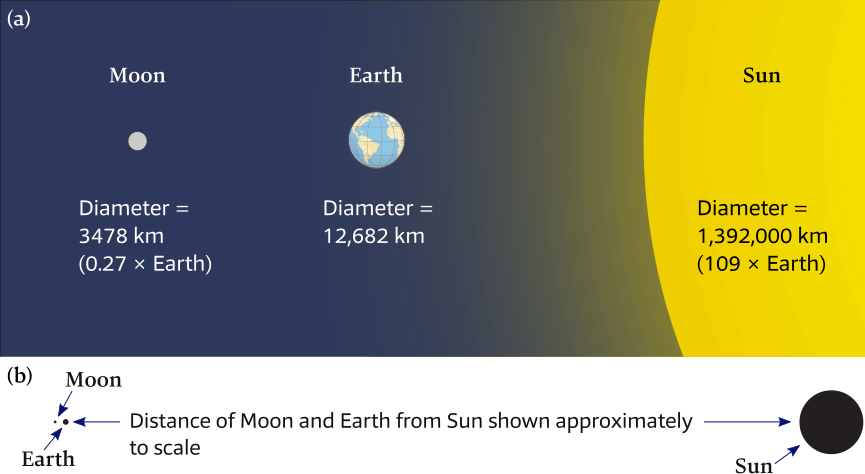
(a) The relative sizes of the Moon, Earth and Sun, showing that the
diameter of the Moon is roughly ¼ that of Earth, while the diameter of the Sun
is 109 times the diameter of Earth.
(b) The relative distances of the Moon, Earth and Sun (approximately to scale).
The solar bulges, however, are much smaller than the lunar bulges. While the Sun is 27 million times more massive than the Moon, its tide-generating force is not 27 million times greater than the Moon’s. This is because the Sun is 391 times farther from Earth than the Moon.
Moon vs Sun tidal effects
Even though the Sun is 391 times farther away from the Earth as the Moon, its force on the Earth is about 175 times larger due to its greater mass, Figure 6.11.
Nevertheless, the Sun's tidal effect is smaller than that of the Moon, because tides are caused by the difference in gravity field across the Earth.
The Earth's diameter is such a small fraction of the Sun – Earth distance that the gravity field changes by only a factor of 1.00017 across the Earth.
This means that the actual force differential across the Earth is 0.00017 × 174.5 = 0.0296 times the Moon's force, compared to 0.068 difference across the Earth for the Moon's force.
The actual Sun's tidal influence (or tidal effect) therefore is 0.0296 / 0.068 = ± 44% of that of the Moon.
Moon + Sun = 1
Moon + 0.44 × Moon = 1
1.44 × Moon = 1
Moon = 1/1.44 = 0.69, so >2/3 of tidal influence.
The solar bulges are only 44% the size of the lunar bulges and, as a result, the Moon exerts over two times the gravitational pull of the Sun on the tides.
This is why the Moon controls tides far more than the Sun: although much smaller in size, it is much closer to Earth.
Earth’s rotation and the tides
The tides appear to move water in toward shore – the flood tide – and to move water away from shore – the ebb tide.
However, according to the nature of the idealized tides presented so far, Earth’s rotation carries various locations into and out of the tidal bulges,
which are in fixed positions relative to the Moon and the Sun.
In essence, alternating high and low tides are created as Earth constantly rotates inside fluid bulges that are supported by the Moon and the Sun.
In an idealized case, the rise and fall of the tides are caused by Earth’s rotation carrying various locations into and out of the tidal bulges.
Tidal variation during the monthly tidal cycle
The monthly tidal cycle is 29 ½ or rather 29.53 days, because that’s how long it takes the Moon to complete an orbit around the Earth. During this orbit, the Moon’s changing position influences tidal conditions on Earth.
The 29 ½ - day monthly tidal cycle is also called a lunar cycle, a lunar month, a lunation or a synodic month.
Synodic
Originally a “synod” was an ecclesiastic council or meeting to consult on church matters.
In astronomy it is a conjunction of two or more of the heavenly bodies; in our case: the Moon meeting up on the same side of the Earth again.
Synodic is the adjective (relating to a synod).
The term comes from Ancient Greek συνοδικός – “related to an assembly, meeting”, from σύν – “with” (syn-) + ὁδός – “way, path” (odos).
Note that a tidal cycle (without the “monthly”) is synonymous with a tidal day: 24 hours 50 minutes 28 seconds.
Sun and Moon combined
Figure 6.12 shows the positions of the Earth, Moon, and Sun at various points during the 29 ½-day lunar cycle.
At the New 🌑︎ Moon (with the Moon in conjunction) and Full Moon 🌕︎ Moon (with the Moon in opposition), the Sun, Earth and Moon are in syzygy [Wiki]: three celestial bodies in a straight line.
Tidal forces act to reinforce each other, and the ocean both rises higher and falls lower than the average, see Figure 6.12 (a).
At this time, the tidal range (the vertical difference between high and low tides) is large, resulting in very high high tides and quite low low tides, because there is constructive interference, see Figure 6.14 (left), between the lunar and solar tidal bulges.
The maximum tidal range is called a spring (springen = to rise up) tide (no connection with the spring season) because the tide is extremely large or “springs forth.”
Conversely, at the first 🌓︎ and third quarter 🌗︎, the Sun, Earth and Moon are at right angles, see Figure 6.12 (b), i.e. in quadrature [Wiki], and tidal forces counteract each other, i.e. there is destructive interference, see Figure 6.14 (right), and the tidal range is smaller than average.
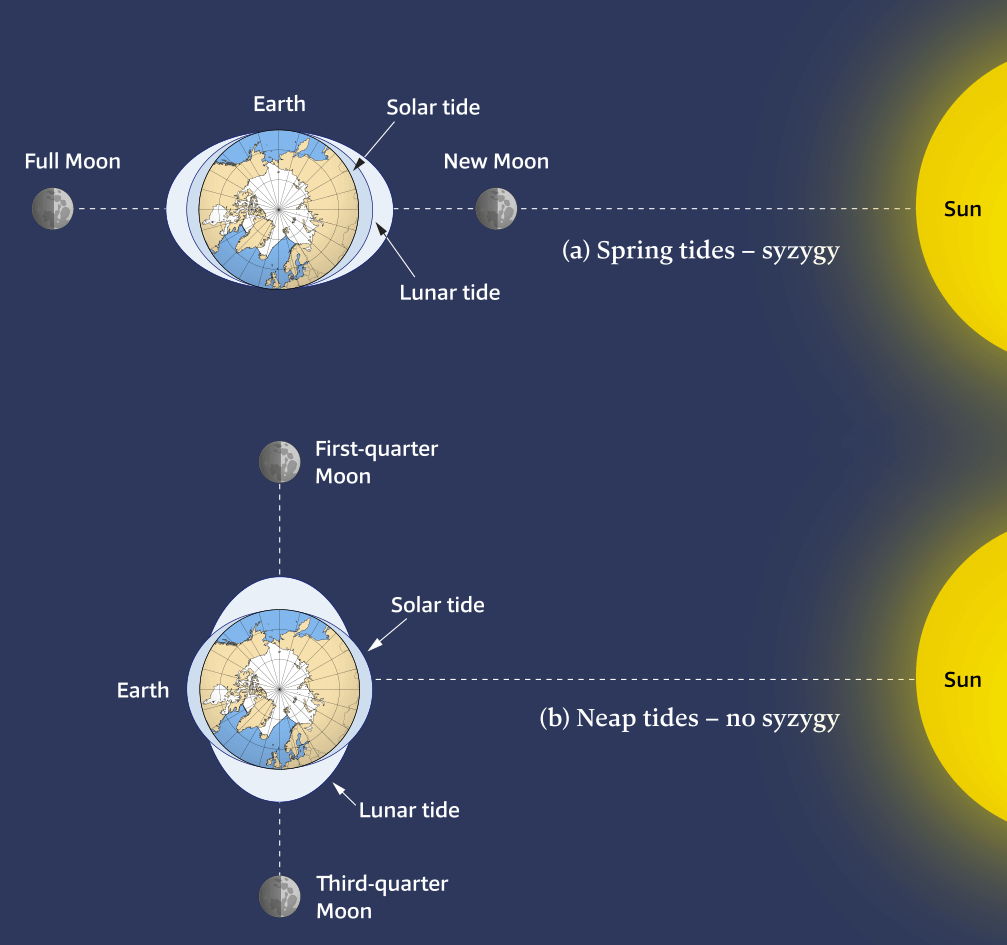
(a) When the Moon is in the new or full position, the tidal bulges created by the Sun and Moon are aligned, there is a large tidal range on Earth, and spring tides are experienced.
(b) When the Moon is in the first- or third-quarter position, the tidal bulges produced by the Moon are at right angles to the bulges created by the Sun. Tidal ranges are smaller and neap tides are experienced. Note that there is only one moon in orbit around Earth.
It is the combined effect of the gravitational forces of the Sun and Moon – which varies during the 29 ½-day lunar cycle – that creates spring and neap tides. When both aligned (i.e. in syzygy) with the Earth they combine their attraction, and otherwise they counteract their attraction.
- Spring tides – word origin: Old English “Springere”, meaning to rise or spring up.
- Neap tides – word origin uncertain: possibly nep = “scarcely” or “barely touching”, as in Old English “nēpflōd”. Otherwise a silly acronym: near even as possible…
- Range is defined as the “difference in water level between high and low tide”.
Spring tides have higher high tides and lower low tides whereas neap tides have lower high tides and higher low tides, see Figure 6.13.
Hence, the range is larger in a spring tide than in a neap tide.
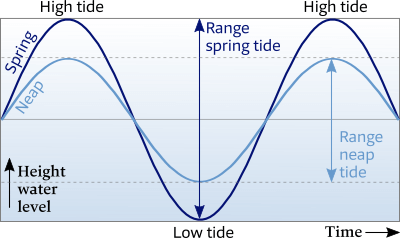
The graph shows the ideal sinusoids of both spring and neap tides.
Vertically the water height is shown versus horizontally the time.
Spring tide and neap tide levels are about 20% higher or lower than average.
Timing of spring and neap tides
Water has mass and therefore momentum. Moreover, it is a viscous fluid that generates friction if moved. Therefore, the actual spring tide lags roughly 36 to 48 hours behind a Full Moon or New Moon occurrence.
The time difference between a spring tide and a neap tide is ±7 days, in accordance with these phases of the Moon: approximately 2 spring and 2 neap tides per calendar month.
Eye candy
- The Beltoforion interactive animation of the Sun – Earth – Moon system with neap tides, spring tides and the various forces involved.
- Videos from NASA: Moon phases - northern hemisphere and southern hemisphere; click the gear icon ⚙︎ and set speed to 2 and quality as high as possible.
Interference
The lunar and solar tidal bulges can be seen as waves, causing constructive interference at spring tides. and deconstructive interference at neap tides. In the section on Moon vs Sun tidal effects it was demonstrated that – despite the Sun's immensely larger mass – the Moon exerts a 2.25 times larger gravitational attraction since the Moon is much closer to the Earth. As a result the solar bulges are much smaller than the lunar bulges and cannot wholly cancel out the lunar bulges – there is no complete deconstructive interference, which means that even at Neap tide there is a tidal range.
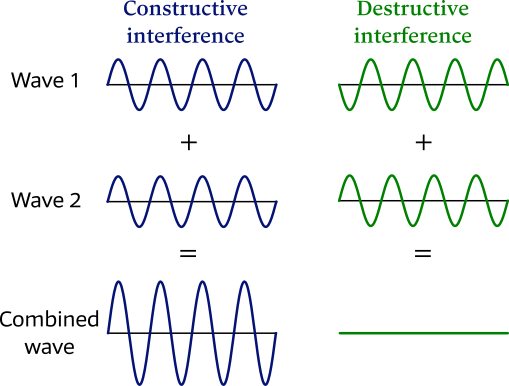
Left: Constructive interference occurs when two waves – or, in this case, two tidal bulges during spring tide – overlap crest to crest and trough to trough.
Right: Conversely, during neap tides there is partial deconstructive interference, matching up crest to trough and trough to crest.
Note that the image shows two waves of equal amplitudes for illustrative purposes, whereas lunar and solar bulges are of dissimilar sizes.
Phases of the Moon
The dramatic changes of the phase of the Moon are shown in Figure 6.15 as the Moon progresses during the monthly tidal cycle.
In between the phases of:
- New Moon 🌑︎ and First Quarter 🌓︎ waxing crescent (wax = “to increase”; crescere = “to grow”).
- First Quarter 🌓︎ and Full Moon 🌕︎ waxing gibbous (gibbus = “hump”).
- Full Moon 🌕︎ and Third Quarter 🌗︎ waning gibbous (wane = “to decrease”).
- Third Quarter 🌗︎ and New Moon 🌑︎ waning crescent.
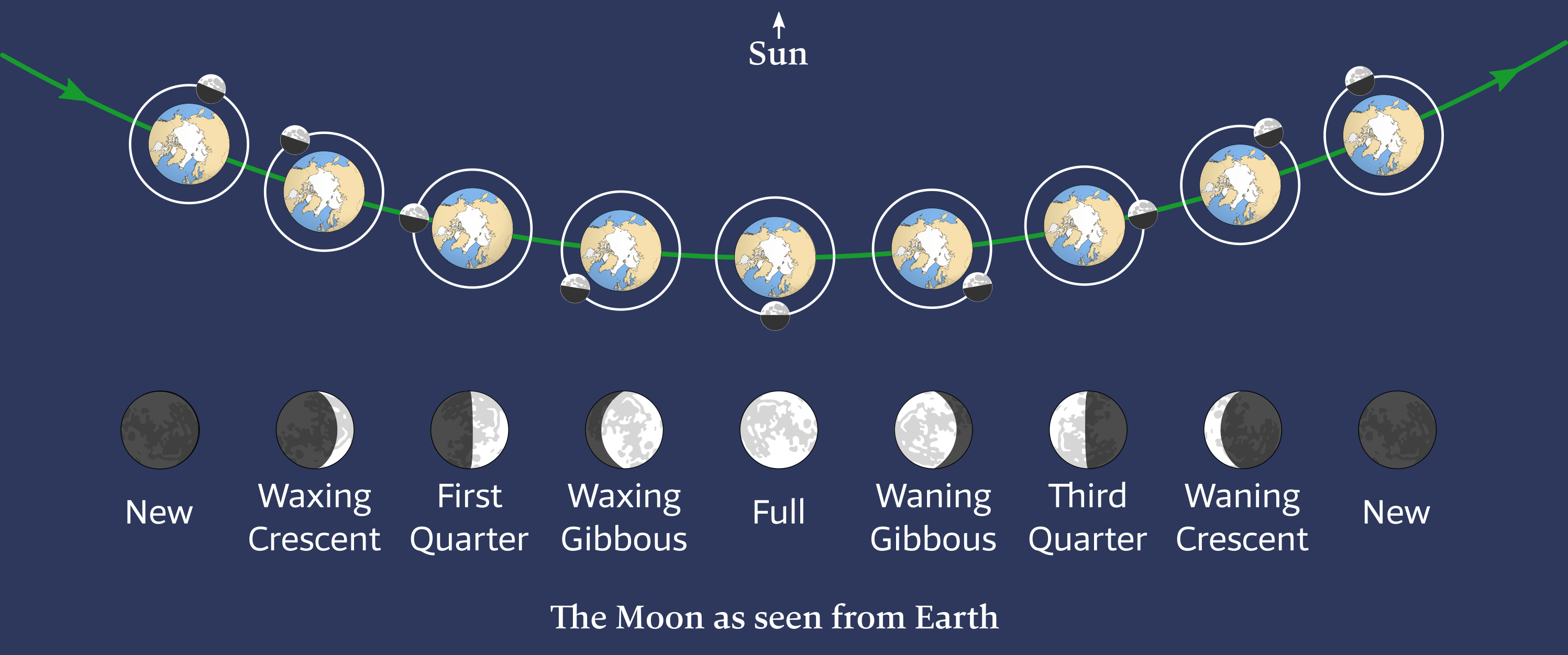

Top: As the Moon moves around Earth during its 29 ½-day lunar cycle, its phase changes depending on its position relative to the Sun and Earth. During a new moon, the dark side of the Moon faces Earth while during a full moon, the lit side of the Moon faces Earth. Top view of the ecliptic, Earth orbiting the Sun, and Moon orbiting the Earth, both counterclockwise.
Bottom: The Moon and phases as seen from Earth.
Earth's rotation drags the position of the tidal bulge ahead of the position directly under the Moon's sublunar point or zenith, and tides are late by about 12 minutes.
The Moon has identical periods of rotation on its axis and revolution around Earth; a property called synchronous rotation. As a result, the same side of the Moon always faces Earth.
Spring vs neap
Spring tides occur during the Full Moon 🌕︎ (in opposition) and New Moon 🌑︎ (in conjunction) phases, when the lunar and solar tidal bulges constructively interfere, producing a large tidal range.
Neap tides occur during the quarter moon phases (First Quarter 🌓︎ and Third Quarter 🌗︎) when the lunar and solar tidal bulges destructively interfere, producing a small tidal range.
Intricacies
Besides the Earth’s rotation and the relative positions of the Moon and the Sun, many other factors influence tides on Earth – five of the most prominent complicating factors being:
- the declination of the Moon and Sun
- the axial tilt of the Earth
- the elliptical shapes of the orbits of the Earth around the Sun, and the Moon around the Earth.
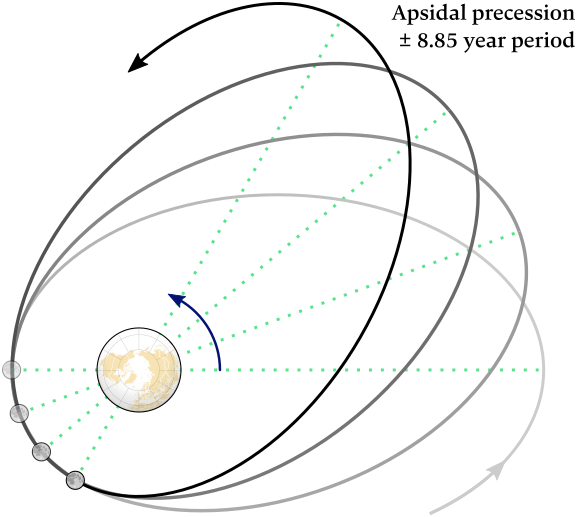
- the apsidal precession of the Moon's orbit; ±8.85 years.
- the nodal precession of the Moon's orbit; ±18.6 years.
Declination of the Moon and Sun
Up to this point, we have assumed that the Moon and Sun have remained directly overhead at the equator, but this is not usually the case. Most of the year, in fact, they are either north or south of the equator.
The angular distance away from the equatorial plane is called declination; from Latin declinare = “to turn away”, “to bend”, “to deviate”. Declination is similar to geographic “latitude”. Note that in Chapter 3 we already saw Magnetic Declination defined as “the angle between Magnetic north and True north”.
Our planet revolves around the Sun along an ellipse in space, and the imaginary plane that contains this ellipse is called the ecliptic; from Ancient Greek ἔκλειψις (ékleipsis, “eclipse”), via ἐκλείπω (ekleípō, “I abandon”, “vanish”) – ἐκ (ek, “out”) and λείπω (leípō, “I leave behind”).
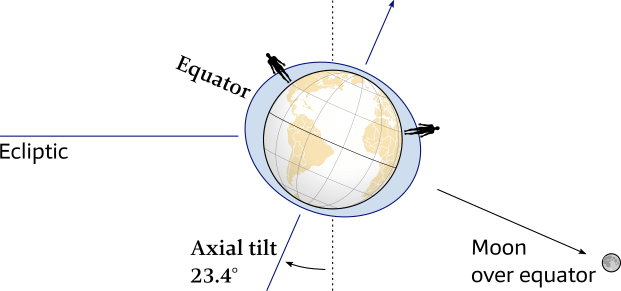
Crucially, the Earth’s axis of rotation is tilted 23.4° with respect to this ecliptic, see Figure 6.17, and it is this tilt that causes the Earth’s seasons as well as some significant tidal pecularities.
It also means the Sun's maximum declination is 23.4°.
The Tropic of Capricorn marks 23.4° S as the most southerly latitude at which the Sun can appear directly overhead at noon, which happens at the December Solstice. Similarly, the Tropic of Cancer marks 23.4° N as the most northerly circle of latitude at which the Sun can be directly overhead, which happens at the June Solstice.
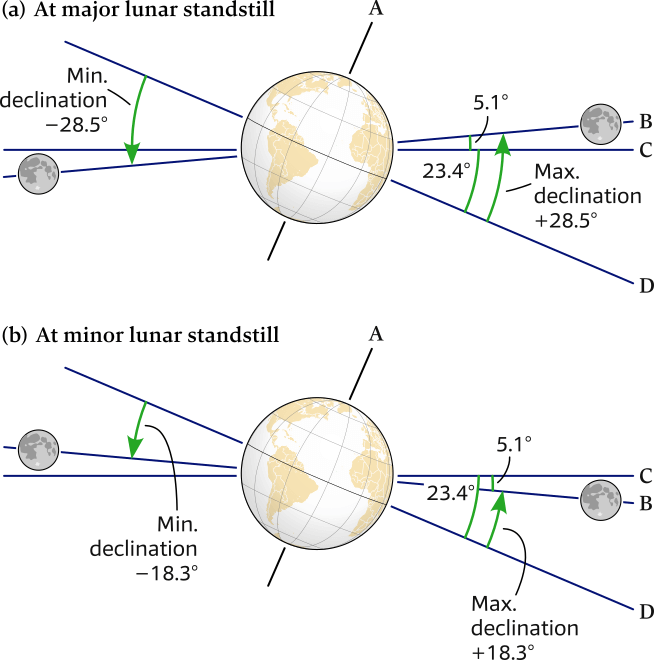
Moon's orbital tilt
To complicate matters further, the plane of the Moon’s orbit is tilted 5.1° with respect to the ecliptic as shown in Figure 6.16. This leads to a maximum declination of the Moon’s orbit of 28.5° (namely, 5.1° plus the 23.4° of the Earth’s tilt), see Figure 6.18.
This declination changes from 28.5° south to 28.5° north and back to 28.5° south of the equator during the multiple lunar cycles within one year.
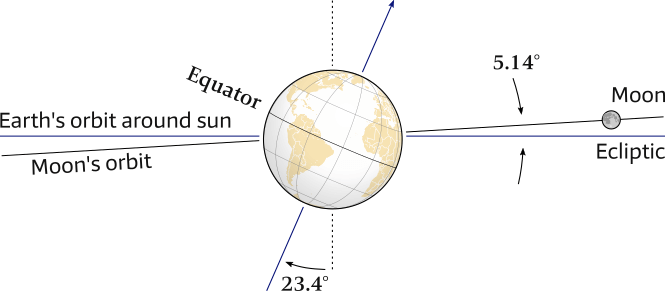
The inclination of the Moon's orbit to the ecliptic is 5.14° and also the Earth's axis is tilted 23.4°, therefore the Moon is only rarely above the Equator, yet has a declination varying between -28.5 S – 28.5° N.
A side view with tidal bulges left out.
The Moon’s orbital path around the Earth is therefore not in line with the equator, except for two days in monthly tidal cycle is 29 ½ days. As the moon completes its orbit around the earth, it is north of the equator for ±14 days, and south of the equator for ±14 days.
This also explains the scarcity of eclipses, see Figure 6.17, since the Sun, Earth and Moon are only occasionally precisely in line.
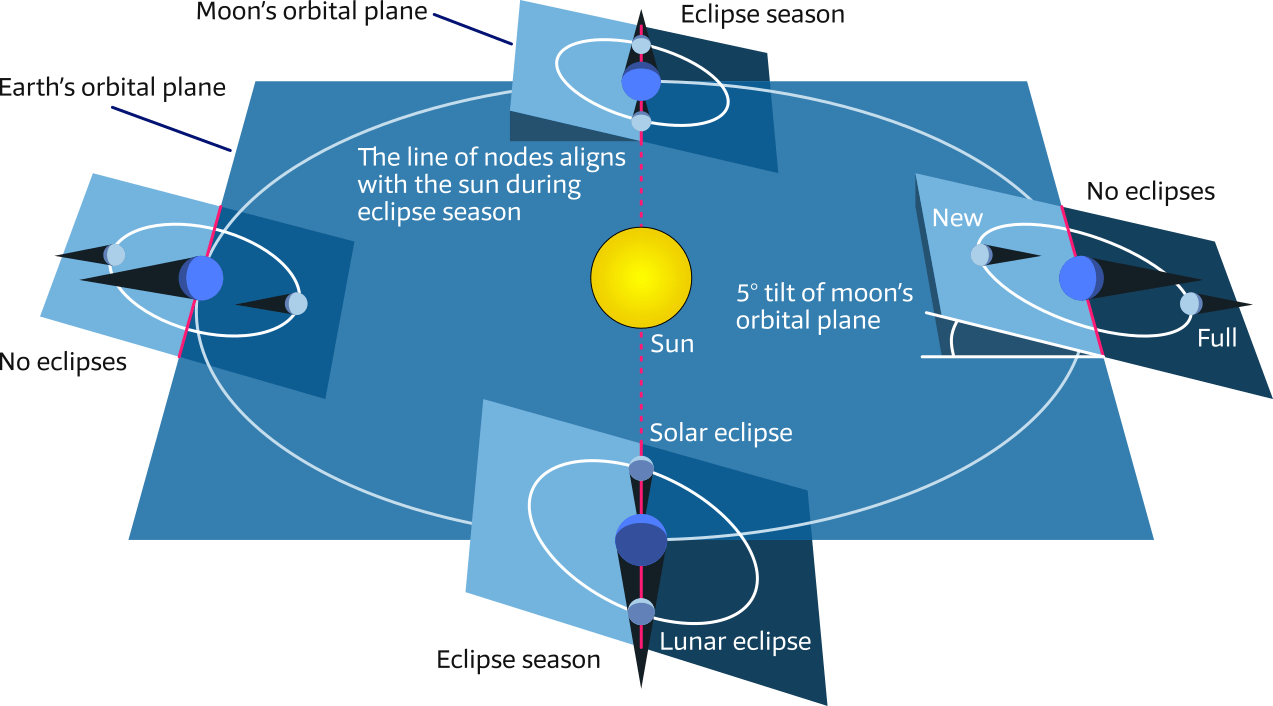
The Sun, Earth and Moon are only occasionally precisely in line.
This is due to the Moon’s orbital tilt of 5.1° with respect to the ecliptic (Earth's orbital plane).
Eclipses are only possible when the line of nodes lies in the ecliptic.
The combined declinations of both the Moon and the Sun mean that tidal bulges are rarely aligned with the equator. Instead, they occur mostly north and south of the equator. The Moon affects Earth’s tides more than the Sun, so tidal bulges follow the Moon, ranging from a maximum of 28.5° south to a maximum of 28.5° north of the equator as shown in Figure 6.18.
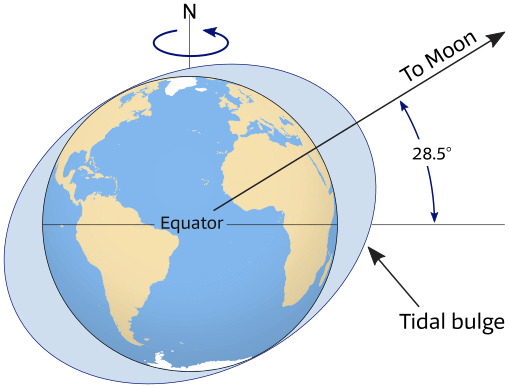
The center of the tidal bulges may lie at any latitude from the equator to a maximum of 28.5 degrees on either side of the equator, depending on the season of the year (solar angle) and the Moon’s position.
Earth's axial tilt
As we saw above, the Earth's axis is tilted 23.4° against the ecliptic. Similar to the equator on Earth, we have the celestial equator on the celestial sphere. The ecliptic intersects the celestial equator at an angle of 23.4°, see Figure 6.19.
The two intersection points are the vernal Equinox and autumnal Equinox.
The two other points on the ecliptic – which are farthest away from the equator – are the summer solstice when the northern hemisphere is facing the Sun and the winter solstice when the southern Hemisphere is facing the Sun.
Usually, the Sun passes through:
- Vernal equinox on March 20
- Summer solstice on June 21
- Autumnal equinox on September 23
- Winter solstice on December 22
These terms have a northern hemisphere biase by pointing at the seasons on the northern hemisphere.
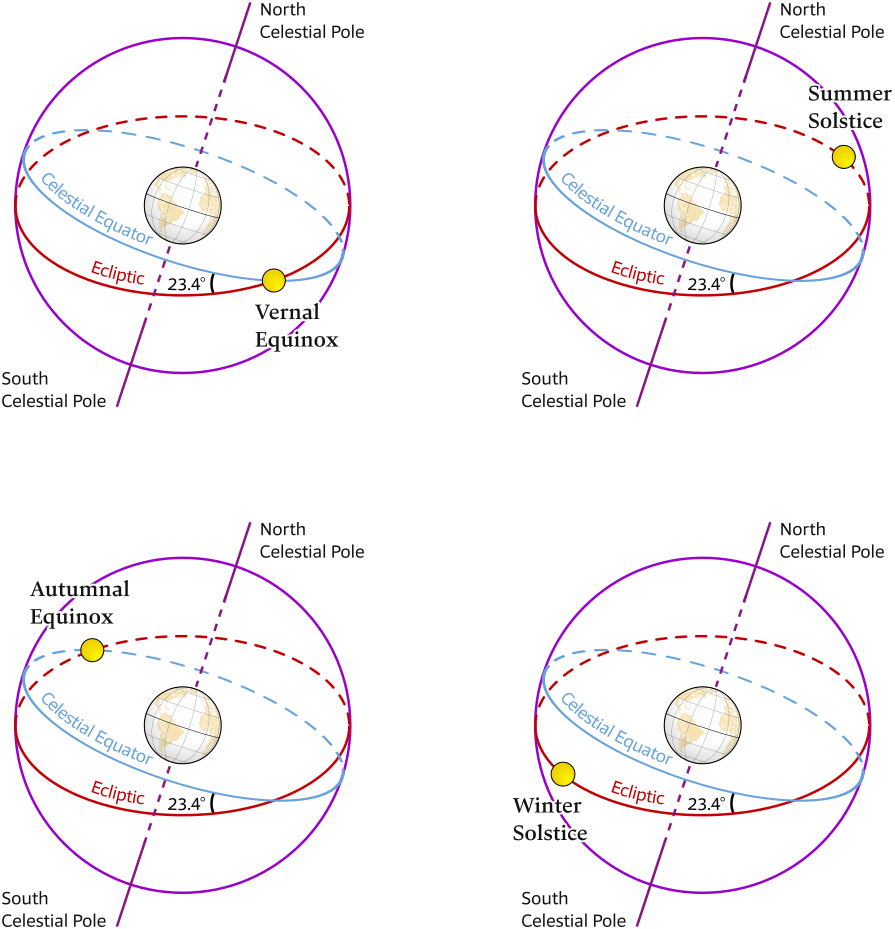
The celestial equator (light blue) is the great circle in which the plane of the terrestrial equator intersects the imaginary celestial sphere (navy blue).
As the Earth orbits around the Sun in one year:
Top left Vernal Equinox (Autumn in southern Hemisphere)
Top right June Solstice (Summer Solstice in northern Hemisphere) when the Sun is most northerly of the equator
Bottom left Automnal Equinox (Spring in southern Hemisphere)
Bottom left December Solstice (Winter Solstice in northern Hemisphere) when the Sun is most southerly of the equator
The Sun's movement in the sky is a like a pendulum
Though experiment :
Without the tilt of the Earth's axis of rotation in relation to our orbit – or equivalently, if the Earth's equatorial plane coincided with the ecliptic plane – every day and for everyone on Earth the path of the Sun would look like an equinox.
Consequently, the Sun would rise due east, set due west, be up for 12 hours and down for 12 hours. The only difference for observers at different latitudes would be the noontime declination of the Sun.
Yet, with the actual tilt of 23.4°, there is the pendulating pattern in the movements of the Sun in the sky.
Like a pendulum, the sunrise direction
changes from NE at summer solstice to SE at winter solstice, and back to NE, completing one full swing back and forth, or one full cycle, each year, see Figure 6.20.
Near the Equinox the sunrise direction changes rapidly from day to day, like the rapid motion of a pendulum at mid-swing, and there is a stopping or “standstill” at solstice, like the outer limit of the swing of a pendulum.
The Sun's declination changes little for the ~2 weeks around solstice. The sunrise and sunset directions change little over this time as well.
The Moon's movement in the sky is the second significant pendulum, and in the section Nodal precession we will discuss the “lunistice” or “lunar standstill“ when the Moon's declination is at its extremes, seemingly standing still.
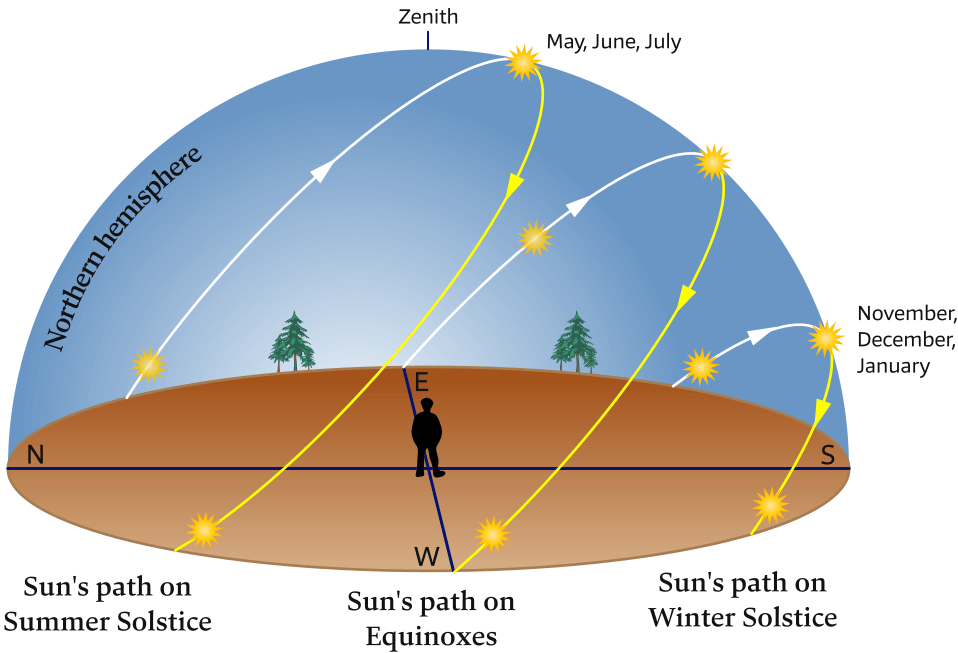
Shown are the daily tracks of the Sun on the solstices and equinoxes, as seen by an observer at mid-northern latitudes. Similar to a pendulum the Sun's path oscillates in the sky while 4 characteristics change:
1 – the sunrise direction
2 – the sunset direction
3 – the length of daylight
4 – the altitude of the Sun at noon above the southern horizon
“Equinox“ is derived from the Latin “aequinoctium“, from “aequus“ (equal) and “nox“ (night). On the day of an equinox, daytime and nighttime are of approximately equal duration all over the planet.
“Solstice“ is derived from the Latin “sol” and “sistere“ (to stand still). An accurate description since at the solstices, the Sun's declination appears to stand still; that is, the seasonal movement of the Sun's daily path (as seen from Earth) pauses at a northern or southern limit before reversing direction.
Declinations of the Sun and the Moon combined
- The Moon’s declination cycle in 29.5 days: a monthly tidal cycle = a lunar cycle = a lunar month = a lunation = a synodic month.
With a maximum swing from 28.5 N to 28.5 S at the major lunar standstill and a minimum swing from 18.5 N to 18.5 S at the minor lunar standstill. - The Sun’s declination cycle ranges from 23.5 N (Summer Solstice) to 23.5 S (Winter Solstice) in a year.
The combined declinations of Earth and Moon influences local tides as shown by the tidal bulges in Figures 6.21.
Note, that these two successive high tides are unequal, and person anywhere on a given latitude would experience two different tidal heights in a row.
Whereas, with the Moon over the equator, see Figure 6.22, two successive high tides are nearly equal.
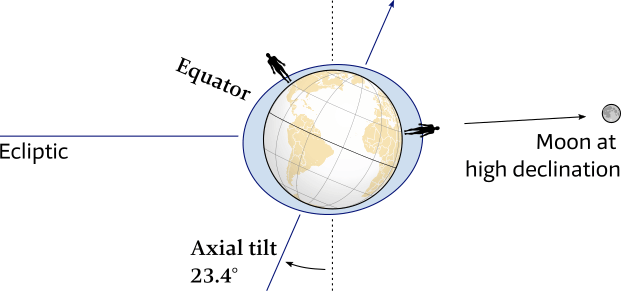
The Earth's axial tilt in combination with the Moon at high declination results in different successive tidal heights.
The Earth's axial tilt in combination with the Moon over the equator results in (nearly) equal successive tidal heights.
Remember that the shown landmasses (also in Figure 6.21) obstruct the model of the “idealized tidal bulges”, see Figure 6.9.
Within one lunar cycle the declination of the Moon turns from maximum north
via the equator (zero degrees)
to maximum south
and back, via the equator, to maximum north.
Over the equator this movement is fast and at the extremes the slowest, apparently standing still: Lunar standstills
Lateron we will see that these maxima oscillate as well within a period of 18.6 years, see Figure 6.31.
Elliptic orbits
The orbits of the Moon around the Earth, and Earth around the Sun are elliptic, and therefore the changes in distances between the bodies cause variations in the tide-raising forces.
For the Moon this variation is significant (14%), yet for the Sun this variation is minimal (3%).
Apsides: Perigee & apogee and perihelion & aphelion
An apsis – from Greek ἁψίς, meaning “arch, vault”; plural “apsides” ἁψῖδες – is an extreme point in a body's orbit, which is nearly always an ellipse, see Figure 6.23
There are two apsides in an elliptic orbit, named with the Greek prefixes peri– (περί meaning “near”) and ap(o)– (ἀπ(ό) meaning “away from”) added to a reference to the celestial body being orbited.
- –gee refers to Earth (Gaia)
- –helion refers to the Sun (Helios)
These two orbits have two apsides each four points:
- perihelion: least distance between the Earth and the Sun, around January 3
- aphelion: greatest distance between the Earth and the Sun, around July 4
- perigee: least distance between the Moon and the Earth
- apogee: greatest distance between the Moon and the Earth
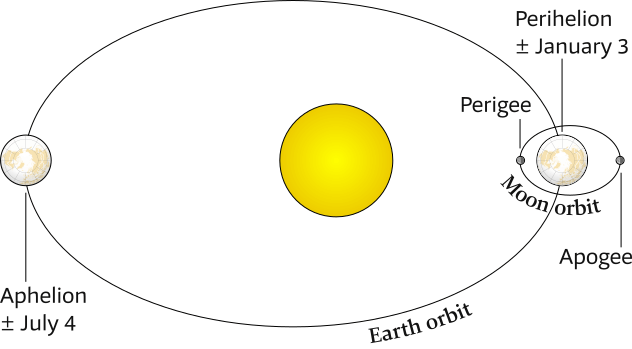
Top view of Earth and Moon orbits with perihelion & aphelion and perigee & apogee.
Distances are not to scale and ellipses are exaggerated.
Although an ellipse, the Earth's orbit around the Sun is very nearly circular.
During the northern Hemisphere winter our planet is 147.1 million km from the Sun, a distance which increases just slightly – with 3.4% – to 152.1 million km in the summer.Tidal ranges are largest when Earth is near the perihelion in January, and smallest near the most distant point (aphelion) in July.
The Moon revolves around Earth in a more elliptical shaped orbit, in which the Earth–Moon distance varies by 14% between 356,500 km at the perigee to 406,700 km at the most distant point (apogee). The Moon cycles between perigee, apogee, and back to perigee in about 27.32 days, the sidereal month.
View the apparent size differences of apogee – perigee moon and
aphelion – perihelion sun.
Perigean spring tides
About three or four times a year – in spring and autumn – the New Moon or Full Moon coincides closely in time with the perigee of the Moon, resulting in a perigean spring tide also colloquially known as a king tide .
The difference between the ranges of a perigean spring tide and a normal spring tide is small: 15 centimeters or 2% maximum, yet large enough to result in the flooding of low-lying coastal areas during high tide. If a storm occurs during this time, damage can be extreme.
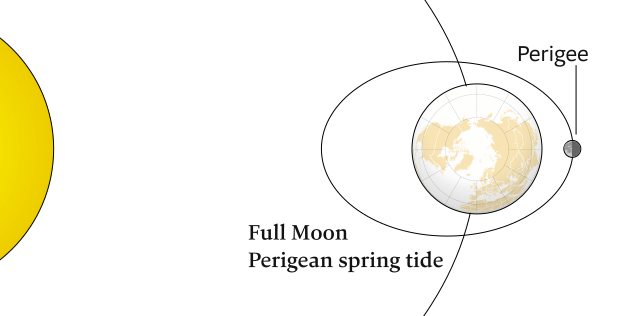
The elliptic orbits of Earth around the Sun and the Moon around Earth change the distances between Earth, the Moon, and the Sun, thus affecting Earth’s tides.
The perigee of the Moon can occur at any point in the orbit around the Earth due to apsidal precession [Wiki], (play around with an interactive animation); for mariners the Full Moon perigee shown in Figure 6.24 and the New Moon perigee shown in Figure 6.25 are of significance.
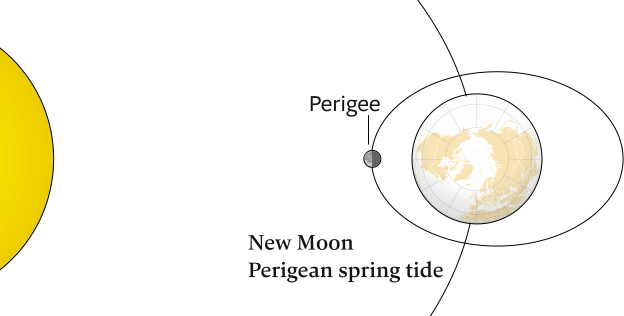
The changes in distances due to the elliptic orbits mean that spring tides have greater ranges during the northern Hemisphere winter than in the summer, and spring tides even have greater ranges when they coincide with a perigee: either the New Moon Perigean (show here) or Full Moon Perigean shown in Figure 6.24.
What about “lunar” or “elliptical”?
- The “Moon's orbit” is not to be confused with a “lunar orbit”, the former is the orbit of the Moon, the latter an orbit around the Moon.
- The adjective “elliptic” is used when describing these orbits, since “elliptical” can also mean: a shape reminding of an ellipse; oval.
Apsidal precession
As we saw in the elliptic orbits section, the Moon's orbit is an ellipse and has therefore two apsides: a perigee (the point of orbit closest to Earth) and an apogee (the point of orbit farthest from Earth).
These two extreme points are connected by the line of apsides, which slowly rotates east, in the same direction as the Moon. This gradual rotation is known as lunar precession, apsidal precession, or cycle of lunar perigee, which completes a full circuit every 8.85 years, see Figure 6.26; causing tidal modulations on an interannual time scale, see Table 6.1.
Twice in this 8.85 year period – approximately every 4.5 years – the perigee points either towards or away from the Sun: so at either the March or September equinox the Moon is both at its closest point to the Earth, and is also overhead at the equator.
Note that this aspect of the Moon's motion is 2-dimensional, and this figure shows a single plane.
The dotted lines are the “lines of apsides” that rotate east each orbit (with forward movement exaggerated).
When the line of apsides points towards the Sun, every ±4.5 years, there are higher tides.
With the angle p measured in degrees longitude, see Chapter 1, maximum tide generating forces are at p = o° (perigean Full Moon at automnal equinox & perigean New Moon at vernal equinox) and p = 180° (perigean Full Moon at vernal equinox & perigean New Moon at automnal equinox).
- Vernal equinox, see Figure 6.19 (top left)
- Automnal equinox, see Figure 6.19 (bottom left)
- Perigean Full Moon spring tide, see Figure 6.24
- Perigean New Moon spring tide, see Figure 6.25
| Table 6.1 – Equinoxes and Dates when mean longitude of Lunar Perigee “p” passes an equinox, vernal (p = 0°) or autumnal (p = 180°); source. | |
|---|---|
| Vernal | 2006 Oct 19 |
| Automnal | 2011 Mar 23 |
| Vernal | 2015 Aug 25 |
| Automnal | 2020 Jan 27 |
| Vernal | 2024 Jun 29 |
| Automnal | 2028 Dec 1 |
| Vernal | 2033 May 6 |
| Automnal | 2037 Oct 9 |
The 8.85 year perigean cycle / apsidal precession represents variation of lunar orientation relative to the Earth – Sun axis in a predominantly “longitudinal” motion.
Increase of tide generating forces occurs when there is Earth – Sun – Moon alignment in both longitude and declination, with the latter mechanism producing equinoctial peak tides for regions experiencing mainly semidiurnal tides.
As the solar declination is away from the equator during the solstices, apsidal precession does not produce a regular harmonic influence on high water levels in regions experiencing mainly diurnal tides.
The additional range provided by apsidal precession is largest (between 0.3 and 0.6 m) in regions dominated by semidiurnal tides where the tidal range is >6 m, notably in the eastern part of the Bering Sea, the Hudson Strait, the Gulf of Panama, on the Patagonian Shelf, the Irish Sea, the Bristol Channel and La Manche / English Channel as well as on the northwest Australian Shelf.
Proportionally, the additional range is at least 5% of the tidal range in most of the world's oceans. In the Caribbean Sea, the additional range is over 15% of the tidal range.
Sea level rise and floodings caused by global warming are exacerbated by apsidal precession, in addition to nodal precession, which described in the next section.
See Wikipedia for rotating of lines of apsides [in general] and lunar absidal precession [regarding our Moon].
Nodal precession
The precession of the line of nodes or nodal precession is the second “wobble” in the Moon's orbit that influences tides.
This motion is best envisioned by a plate or coin spinning on a table, yet pulling it through the table, cutting it in half, so that instead of one point touching the table it has two end points (nodes) of the nodal line sharing with the table.
While the plate or coin keeps spinning, this line of nodes rotates.
Obviously, the term “wobble” is polysemantic, since the Moon has several types of precessions, e.g. the apsidal precession we just covered.
Here be dragons 🐉︎
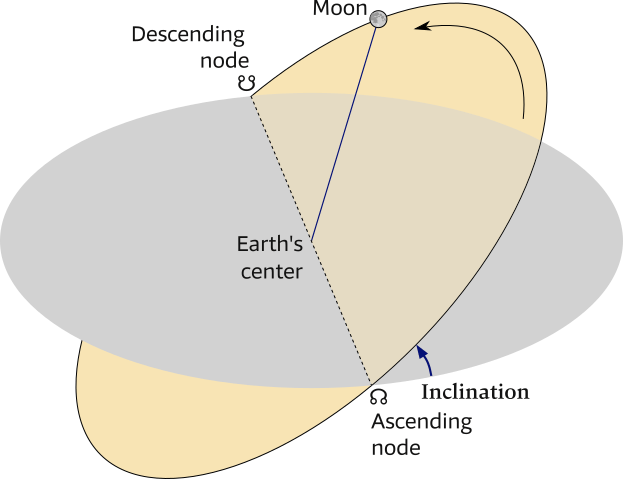
Figure 6.27 shows the lunar nodes, which are the points where the orbit of the Moon crosses the ecliptic, as well as the line of nodes (the nodal line) where both planes intersect.
The ascending node, where the Moon rises above the ecliptic, is historically referred to as the dragon's head ☊︎ (Latin: caput draconis).
Similarly, the descending node, where the Moon sets below the ecliptic, is known as the dragon's tail ☋︎ (cauda draconis).
The orientation of the line of nodes changes as the Earth – Moon system revolves around the Sun: twice a year the line of nodes points towards the Sun, and twice a year in the direction of the Earth's orbit; examine this nodal precession animation.
A full 360° precession of nodes takes ±18.61 years, see Figure 6.28, and the period of time between two consecutive passages of the Moon through the same node is known as a nodal month, draconic month or draconitic month (27 days, 5 hours, 5 minutes, 35.8 seconds).
Again, we are referring to dragons, like hic sunt draconis [Wiki] and not “draconian” (after Draco [Wiki], the first legislator of Athens).
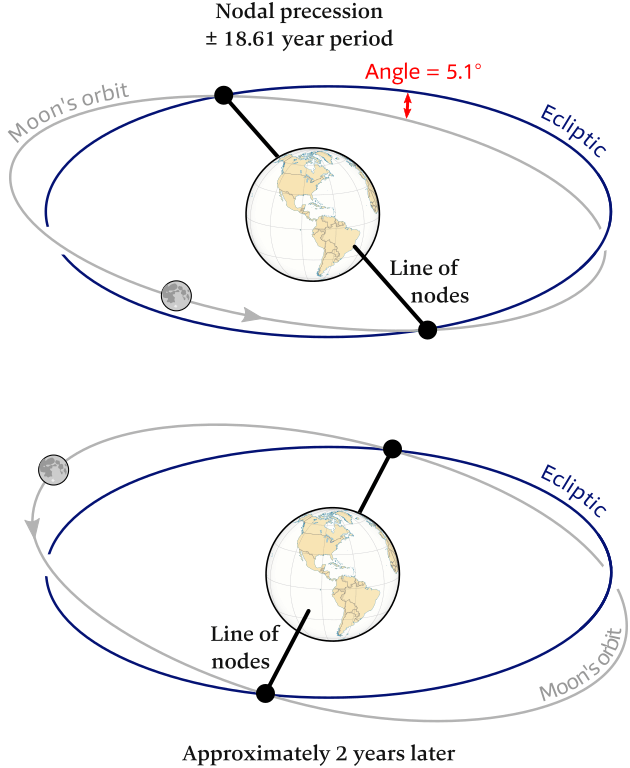
While the angle between the two planes stays 5.1°, the line of nodes rotates. This “nodal precession” is almost 19 times slower than a full orbit of the Earth around the Sun, so twice each solar year the line of nodes points towards the Sun.
See below for an animation of nodal precession.
Similar to a solstice, there is the “lunistice” or lunar standstill [Wiki] when the Moon is seemingly standing still with little change in the outer extremes of monthly range of rising / setting directions and declination.
- While the standstill at solstice is about 2 weeks, the lunar standstill is almost 3 years.
- Figure 6.29 shows the 2 lunar standstills:
- Major lunar standstill – maximum range of Moon rising / setting, when the declinations of the Sun and the Moon amplify each other:
23.4° + 5.1° = 28.5°. - Minor lunar standstill – minimum range of Moon rising / setting, when the declinations counteract each other:
23.4° − 5.1° = 18.3°.
- Major lunar standstill – maximum range of Moon rising / setting, when the declinations of the Sun and the Moon amplify each other:
A half period of 9.3 years separates these two standstills, Table 6.2 lists the years when Major / Minor standstills are at their extremes.
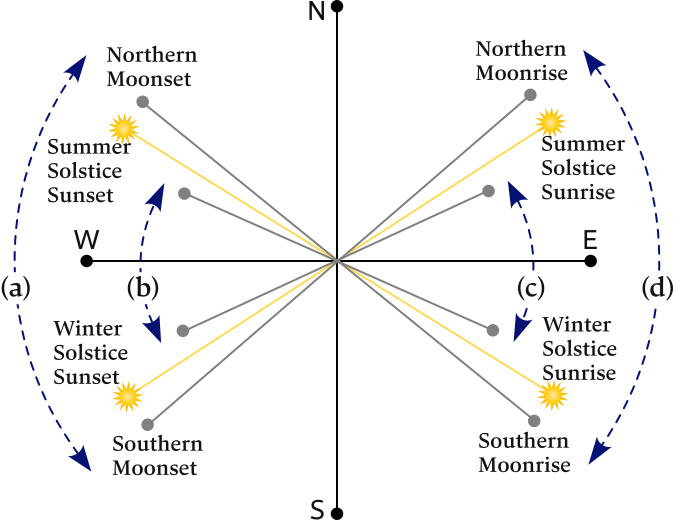
(a) and (d) Moonset and moonrise ranges at major standstill are larger than the sunset and sunrise ranges. The Moon will appear highest in the sky as the Moon's declination (effectively the latitude on the sky, see prior mentioned definition) swings each month between circa −28.5° and +28.5°.
(b) and (c) Moonset and moonrise ranges at minor standstill are smaller than the sunset and sunrise ranges. The Moon will appear lowest in the sky as the Moon's declination swings each month only between circa −18.3° and +18.3°, see also Figure 6.30.
| Table 6.2 – Dates of Major / Minor lunar standstills and Declinations (considering other wobbles / precessions as well), source. | ||
|---|---|---|
| Major | 2006 Mar 22 | ±28.725 |
| Minor | 2015 Jan 18 | ±18.577 |
| Major | 2025 Mar 22 | ±28.719 |
| Minor | 2034 Dec 12 | ±18.553 |
| Major | 2043 Sep 12 | ±28.703 |
| Minor | 2052 Jan 28 | ±18.646 |
The “” in front of the years 2015, 2034, 2052 forewarns us that the Moon’s orbital excursion above or below the equator takes the minimum value of circa 18.3 degrees, which occurs at the minor lunistice. This slightly increases the chances of the moon being directly overhead at the equator coinciding with the other factors that contribute to extreme tidal forces.
In some places, these extreme tidal conditions can cause water levels to be 0.5 m higher than a normal spring tide, see e.g. the National Oceanography Centre.
Looking back at Figure 6.21 (Moon at high declination) and Figure 6.22 (Moon at low declination) it will be come clear that
the semidiurnal tide is strong when the lunar declination is small.
The two high-water bulges are close to the equatorial plane during the Moon's revolution and
the Earth's rotation then generates two similar tidal pulses every 24 h 50 m.
In contrast, if the lunar declination is large, the water bulges are on average further remote from the equator. Earth's rotation then generates a tidal signal with a significant diurnal component, i.e. with one tidal pulse every 24 h 50 m.
Consequently, the semidiurnal tide and the diurnal tide each have a maximum once in the lunar nodal cycle of 18.6 years, with an interval of about 9.3 years between both maxima.
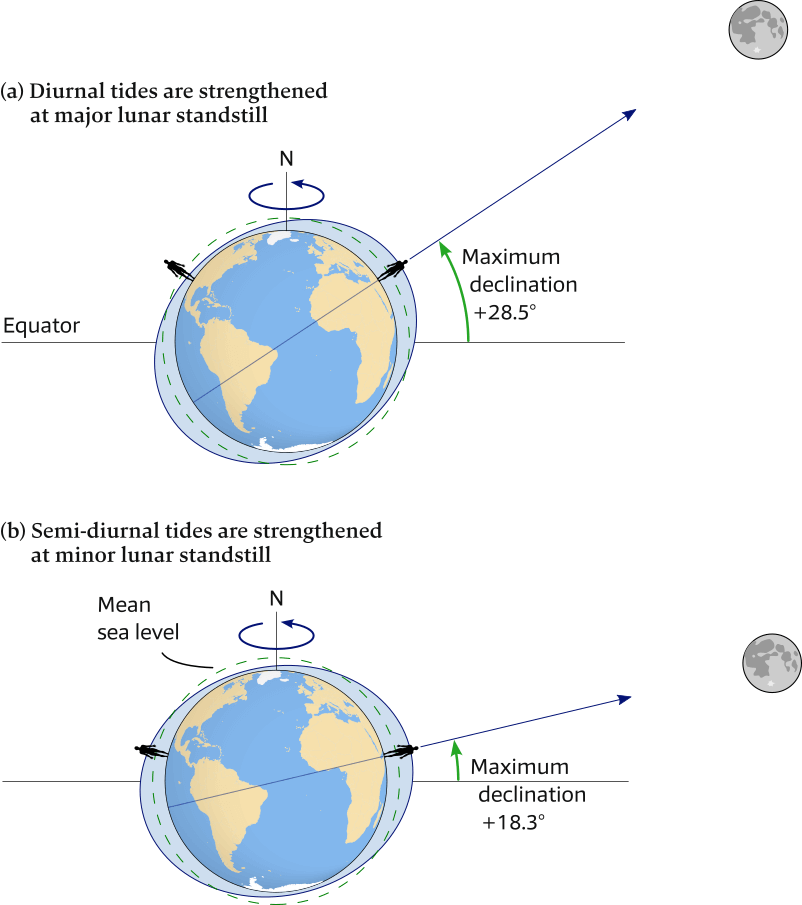
- High declinations of the Moon strengthen diurnal tides.
- Low declinations of the Moon strengthen semi-diurnal tides.

(a) Major lunar standstill: at this maximum extreme the declinations reach around 28.5° south and north.
(b) Minor lunar standstill (9.3 years later): at this minimum extreme the declinations reach only around 18.3° south and north.
Review Figure 6.29 – the directions of the moonsets and moonrises.
A – the Earth's rotational axis.
B – the plane of the Moon's orbit around the Earth (edge on), with the Moon shown at two diametrically opposite positions (Earth – Moon distance not to scale).
C – the plane of the Earth's orbit around the Sun (edge on), i.e. the ecliptic.
D – the plane of the Earth's equator (edge on).
In the section on types of tidal patterns we will learn that most of the world's coastlines have semidiurnal tides.
This means that in half of the Moon’s 18.6-year cycle, our coastal daily tides are suppressed [which is the current situation] especially at the three years around 2025: high tides are lower than normal, and low tides are higher than normal, see Figure 6.31 (a).
In the other half of the cycle – [which is the forthcoming situation] especially at the three years around 2034 – tides are amplified: high tides get higher, and low tides get lower, see Figure 6.31 (b).
(a) Large declinations (major lunar standstill): a bulge passes through each point of the corresponding high latitudinal contour once a day, due to Earth’s rotation: diurnal tidal pattern is enhanced.
(b) Small declinations (minor lunar standstill): a bulge passes through each point of a low latitudinal contour twice a day: semi-diurnal tidal pattern is enhanced.
Climate crisis and the 18.6 year cycle
Despite the heating up of the oceans, there is currently relatively little rise of sea level [Wiki], mainly because we are just past the middle of a 9.3-year dampening of the sea level rise, due to the effects of the moon’s orbital tilt and the precession of the orbital nodes.
By contrast, see table 6.2, in 2025 – 2035 we will face a 9.3-year-long enhancement of sea level rise.
The influence of the 18.6 year cycle on the tides is on average about 5 cm.
That may not seem like much, however the total amount of global average sea level rise over the last decade is also about 5 cm.
That means that nodal precession has roughly the same impact on the height of high tides as the most recent decade of sea level rise caused by climate change.
Moreover, the levels of spring and neap tides are about 20% higher or lower than average sea levels at and near the minor lunar standstill (2035).
Since most coasts have mesotidal ranges – see the section on tidal ranges – of just over 2 meters, 20% = 40 cm, and 5 cm is therefore significant.
The last time that the moon’s orbit exacerbated tidal flooding was in 2015, recall the Chausey archipelago photos. The National Oceanic and Atmospheric Administration recorded already than 600 tidal floods in the USA in 2019, even when the amplification effect from the moon’s orbit was less than it was in 2015. Global sea level rise – due to climate crisis [Wiki] – pushes high tides in only one direction: higher. Therefore, half of the 18.6-year lunar cycle counteracts the effect of sea level rise on high tides, and the other half increases the effect, see the Sea Level Projection Tool [NASA map]. Starting in the mid-2030s, human-made climate change on top of low lunar declinations will lead to high tide floods that can even occur in clusters lasting a month or longer.
References
- Global influences of the nodal cycle and cycle of lunar perigee – 18.61 year and 8.85 year on high tidal levels
- Change of High Water levels by up to 30 cm – the 18.61 year nodal tidal cycle
- Effect of the 18.6-year lunar nodal cycle on tides
Visualizations
Watch the following demystifying animations:
- Line of nodes regression [Youtube]
- The Moon's orbital plane precession in 18.6 years [Youtube, more detailed]
Ancient Greek knowledge
Unlike the planetary orbits, the eccentricities of the Moon's orbit are sufficiently large that they are easily apparent to the naked eye.
The ancient Greeks knew that the lunar perigee precesses – i.e. in the same direction as the Moon – a full 360° every 8.85 years.
Moreover, they noticed that the lunar nodes regress – i.e. in the opposite direction – a full 360° every 18.6 years.
Idealized tide prediction
With an ideal ocean and ideal earth – where the declination of the Moon determines the position of the tidal bulges – we can make an idealized tide prediction.
Figure 6.32
illustrates that the Moon is directly overhead at 28° north latitude when its declination is 28° north of the equator.
If you stand at this latitude when the Moon is directly overhead, it will be high tide, see Figure 6.32 (a).
Low tide occurs 6 lunar hours later (6 h 12 m 30 s solar time), as shown in Figure 6.32 (b).
Another high tide, but one much lower than the first, occurs 6 lunar hours later, as shown in Figure 6.32 (c).
Another low tide occurs 6 lunar hours later, see Figure 6.32 (d).
Six lunar hours later, at the end of a 24-lunar-hour period (24 h 50 m solar time), you will have passed through a complete lunar-day cycle of two high tides and two low tides.
The graphs in Figure 6.32 (e) show the heights of the tides observed during the same lunar day at 28° north latitude, the equator, and 28° south latitude when the declination of the Moon is 28° north of the equator.
Tide curves for 28° north and 28° south latitude have identically timed highs and lows, but the higher high tides and lower low tides occur 12 lunar hours later. The reason that they occur out of phase by 12 lunar hours is because the bulges in the two hemispheres are on opposite sides of Earth in relation to the Moon.
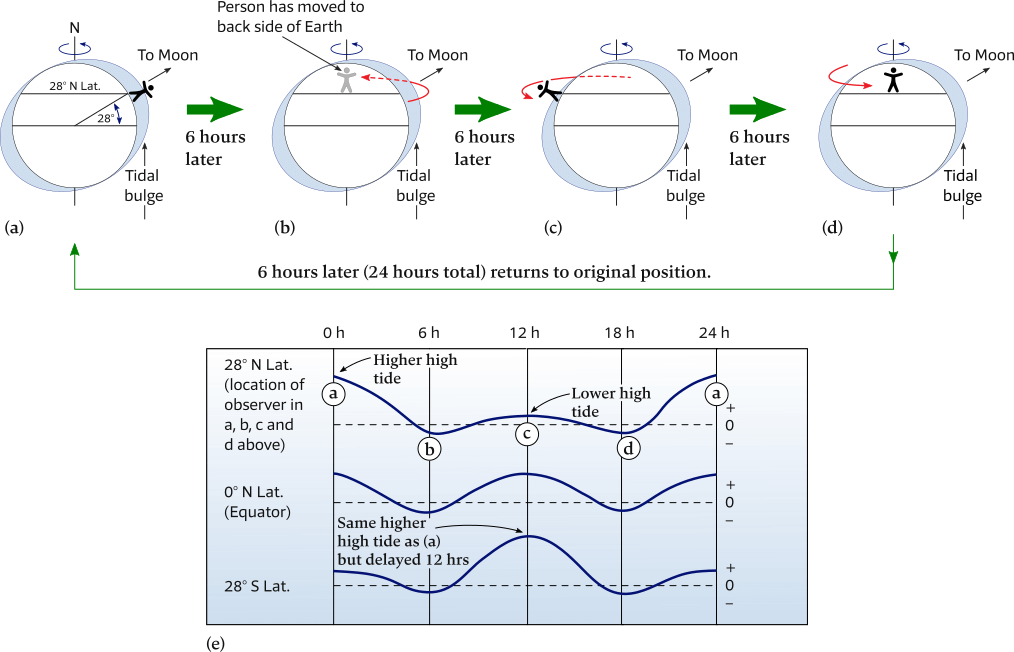
(a) – (d) Sequence showing the tide experienced every 6 lunar hours at 28° north latitude when the declination of the Moon is 28° north.
(e) Tide curves for 28° north, 0°, and 28° south latitudes during the lunar day shown in the sequence above.
The tide curves for 28° north and 28° south latitude show that the higher high tides occur 12 lunar hours (12 h 25 m solar time) later.
Summary of characteristics of the tides on the idealized Earth
- Any location (except the poles) will have two high tides and two low tides per lunar day.
- Neither the two high tides nor the two low tides are of the same height because of the declination of the Moon and the Sun (except for the rare occasions when the Moon and Sun are simultaneously above the equator).
- Monthly and yearly cycles of tidal range are related to the changing distances of the Moon and Sun from Earth.
- Each week, there would be alternating spring and neap tides. Thus, in a lunar month, there are two spring tides and two neap tides.
Tides offshore and in the ocean
If tidal bulges are wave crests separated by a distance of one-half Earth’s circumference – about 20,000 km – we would expect the bulges to move across Earth at about 1600 km/h.
Tides, however, are an extreme example of shallow-water waves, so their speed is proportional to the water depth. For a tide wave to travel at 1600 km/h, the ocean would have to be 22 km deep. Instead, the average depth of the ocean is only 3.7 km, limiting the speed of tidal bulges.
Based on the average ocean depth, the average speed at which tide waves can travel across the open ocean is only about 700 km/h.
Thus, the idealized bulges that are oriented toward and away from a tide-generating body cannot exist because they cannot keep up with the rotational speed of Earth. Instead, ocean tides break up into distinct units called cells.
Amphidromic points and cotidal lines
In the open ocean, the crests and troughs of the tide wave rotate around an amphidromic point – derived from Ancient Greek ἀμφίς (amphís, “around”) and δρόμος (drómos, “running”) – near the center of each cell.
There is essentially no tidal range at amphidromic points, but radiating from each point are cotidal (co = “with”, tidal = “tide”) lines, which connect all nearby locations where high tide occurs simultaneously.
The labels on the cotidal lines in Figure 6.33 indicate the time of high tide in hours after the Moon crosses the Greenwich Meridian.
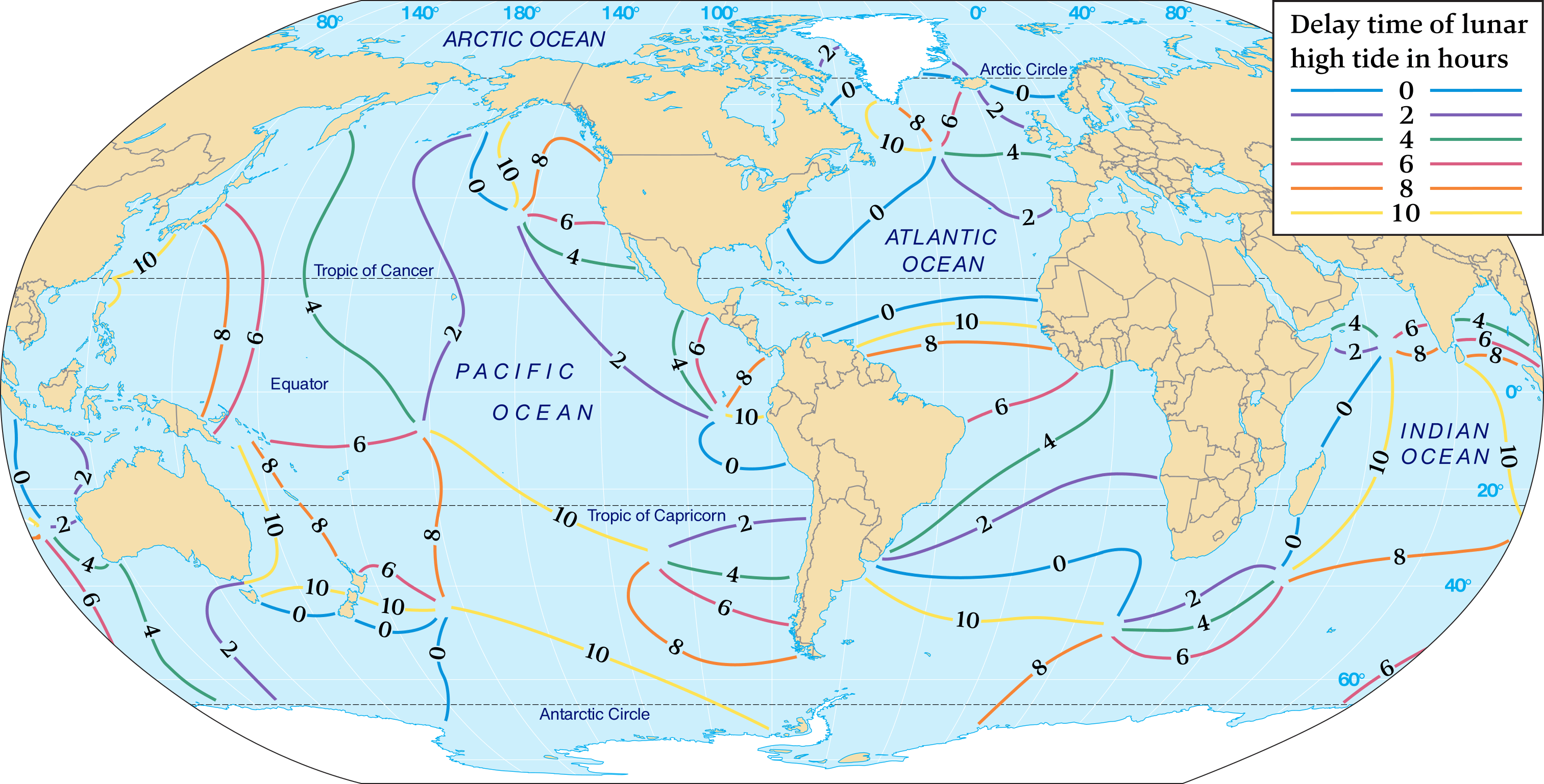

Cotidal lines indicate times of the main lunar daily high tide in lunar hours after the Moon has crossed the Greenwich Meridian (0 degrees longitude).
Tidal ranges generally increase with increasing distance along cotidal lines away from the amphidromic points. Where cotidal lines terminate at both ends in amphidromic points, maximum tidal range will be near the midpoints of the lines.
The times in Figure 6.33 indicate that the tide wave rotates counterclockwise in the northern Hemisphere and clockwise in the southern Hemisphere. The wave must complete one rotation during the tidal period (usually 12 lunar hours), so this limits the size of the cells. Low tide occurs 6 hours after high tide in an amphidromic cell. If high tide is occurring along the cotidal line labeled “10”, for example, then low tide is occurring along the cotidal line labeled “4”.
Effect of the continents
The continents affect tides, too, because they interrupt the free movement of the tidal bulges across the ocean surface. The ocean basins between continents have free standing waves set up within them. The positions and shapes of the continents modify the forced astronomical tide waves that develop within an ocean basin. In fact, two of the most important factors that influence tidal conditions along a coast are coastline shape and offshore depth.
In addition, increased turbulent mixing rates in deep water over areas of rough bottom topography are associated with internal waves created by tides breaking on this rough topography and against continental slopes. These tide-generated internal waves have recently been observed along the chain of Hawaiian Islands, have heights of up to 300 meters, and contribute to increased turbulence and mixing, which strongly affect the tides.
Other considerations
A detailed analysis of all the variables that affect the tides at any particular coast reveals that nearly 400 factors are involved, which are far more than can adequately be addressed here. One of the results of these factors, however, is that high tide rarely occurs when the Moon is at its highest point in the sky. Instead, the time between the Moon crossing the meridian and a corresponding high tide varies from place to place.
Because of the complexity of the tides, a completely mathematical model of the tides is beyond the limits of marine science. Instead, a combination of mathematical analysis and observation is required to adequately model the tides.
Types of tidal patterns
In theory, most areas on Earth should experience two high tides and two low tides of unequal heights during a tidal day of 24 h 50 m.
In practice, however, the various depths, sizes, and shapes of ocean basins modify tides so they exhibit four different tidal patterns in different parts of the world.
These four types, which are illustrated in Figure 6.34, are diurnal [rare], semidiurnal [most common], mixed diurnal [rare] and mixed semidiurnal [common].
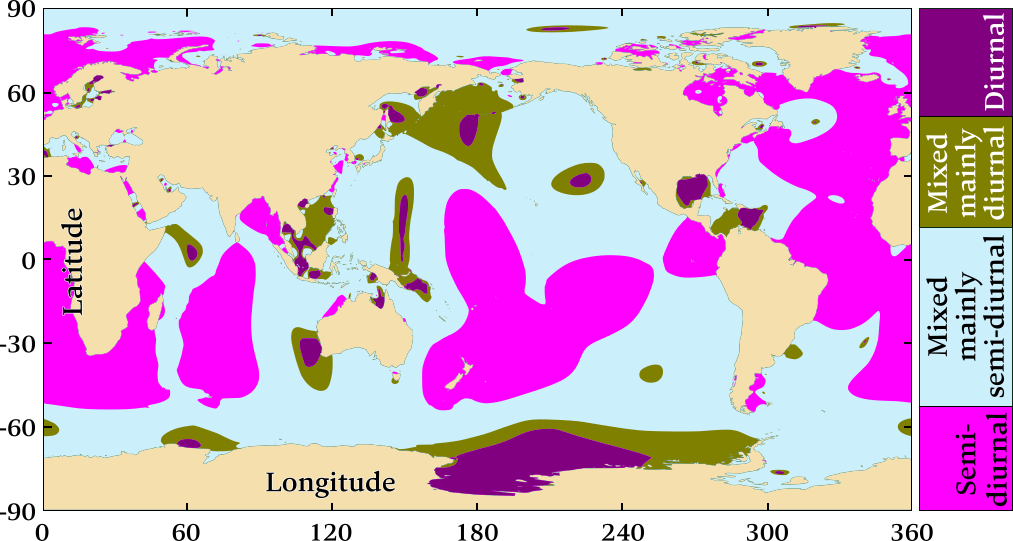
Diurnal and mixed diurnal tides are the isolated exceptions.
Indeed, on a planet with a continouous ocean not blocked by continents, semidiurnal patterns – two high waters per day, in accordance with the moon's orbit – would be default. In practice, most of the world's coastlines have semidiurnal or mixed semidiurnal tides.
- Semidiurnal most common
- Diurnal rare
- Mixed semidiurnal common
Large continents block the westward passage of the tidal bulges as the Earth rotates, and unable to move freely around the globe, these tides establish complex patterns within each ocean basin that often differ greatly from tidal patterns of adjacent ocean basins or other regions of the same ocean basin.
Furthermore, ocean currents, constrained waterways, friction, archipelagos, the Coriolis effect, and coastal topography (headlands, shoals, reefs) influence the rise and fall of the sea level.
As a result different tidal patterns can be experienced in different regions of the world.
Semidiurnal tidal pattern
A semi-diurnal or semidiurnal tidal pattern consists of two nearly equal high tides and two nearly equal low tides within the tidal day –
“nearly”, since tides are always growing higher or lower at any location due to the spring-neap tide sequence, successive high tides and successive low tides can never be exactly the same at any location.
The tidal period is 12 hours and 25 minutes: from high tide to the next high tide. If the planet was covered entirely with water and without any continents obstructing the free motion of water, semidiurnal patterns would be default.
Most of the world's coastlines have semidiurnal tides.
The term “diurnal” can mean “during the day” – as an antonym of “nocturnal” – but with respect to tides it means “having a daily pattern that is completed every 24 hours”, and the prefix “semi” means “half”, see Semi–, Hemi–, Demi–.
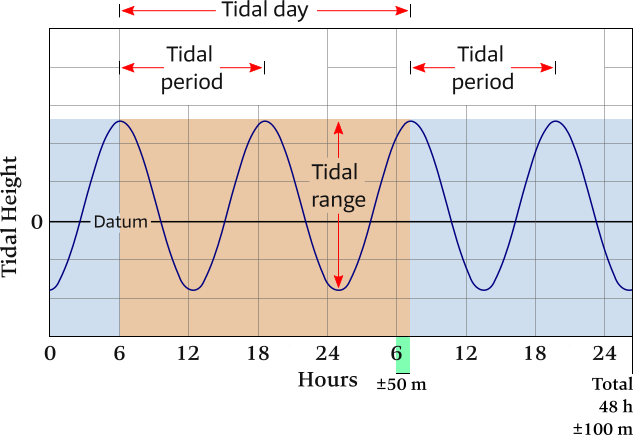
Horizontally the time is shown: a total of 2 tidal days (48 h 100 m 56 s on average), with vertically the heights above or below a reference plane: datum.
The tidal period is the time between successive high waters, so with a semi-diurnal pattern the tidal period (12 h ±25 m) is half of the tidal day.
Diurnal tidal pattern
A diurnal tidal pattern has a single high and a single low tide each tidal day.
The tidal period is 24 hours and ±50 minutes and therefore twice as long as with the semidiurnal tidal pattern.
Diurnal tides can only be found in the Gulf of Mexico, short stretches of Australian coasts, parts of the Caribbean and on the east coast of the Kamchatka Peninsula.
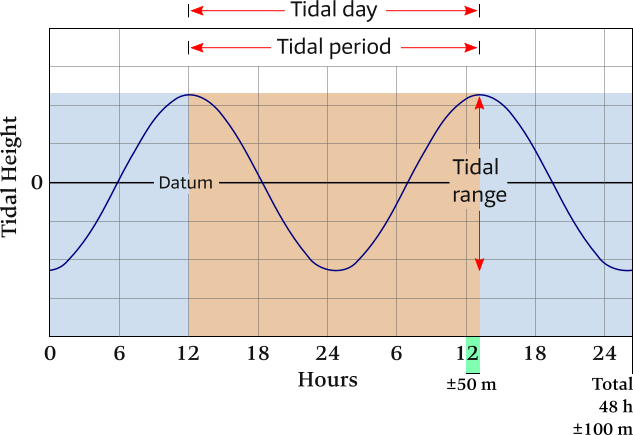
Horizontally the time is shown: a total of 2 tidal days (48 h 100 m 56 s on average), with vertically the heights above or below a reference plane: datum.
Every 24 h 50 m 28 s on average the pattern repeats, which is the tidal day.
The tidal period is the time between successive high waters, so with a diurnal pattern these two time spans are of equal lengths.
Mixed semidiurnal tidal pattern
A mixed tidal pattern may have characteristics of both diurnal and semidiurnal tides, the former is rare, hence this pattern is often described as mixed semidiurnal.
Successive high tides and / or low tides will have significantly different heights, a condition called diurnal inequality.
Mixed tides have a tidal period of 12 hours 25 minutes, but they may occasionally exhibit diurnal periods.
Mixed tides are the most common type in the world, including along the Pacific Coast of north America, the Caribbean, in parts of Australia and in south east Asia.
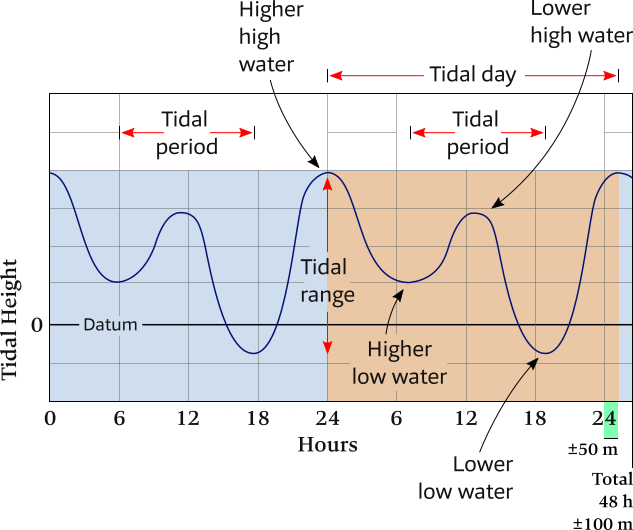
Horizontally the time is shown: a total of 2 tidal days (48 h 100 m 56 s on average), with vertically the heights above or below a reference plane: datum.
Since a mixed diurnal pattern is rarely encountered, during each tidal day there are two high waters and two low waters, all with significanty different heights.
The semidiurnal indicates a 12 h 25 m tidal period and mixed indicates the alternating Higher high water with Lower high water as well as Higher low water with Lower low water.
Key Concept
- Diurnal tidal pattern: one high and one low tide each tidal day (24 h ±50 m).
- Semidiurnal tidal pattern: two high and two low tides each tidal day of about the same height.
- Mixed tidal pattern: usually two high and two low tides of different heights each tidal day, but may also exhibit diurnal characteristics.
Tidal ranges
Besides the tidal pattern also the tidal range – the amplitude of the tide – is consequential to mariners.
Explore this zoomable and adaptable world map of tidal ranges
In France, a unique way of expressing the amplitude of the tide is to use an indicator called the “tidal coefficient”,
indicating the significance of the tide at a given time. It is a dimensionless number, usually between 20 and 120.
- Coefficient 120 – Extraordinary spring tides of equinox
- Coefficient 95 – Mean spring tides
- Coefficient 70 – Mean tides
- Coefficient 45 – Average neap tides
- Coefficient 20 – Lowest neap tides
The Bay of Mont Saint-Michel
For instance, on Saturday 21 March 2015 in the Bay of Mont Saint-Michel an extreme tide ocurred with an coefficient of 119, see the Chausey photos, with a tidal range of 14.15 meters. The next “Extraordinary spring tides of equinox” will take place in March 2033.
These tidal extremes are due in part to the low depth of the bay, the Coriolis forces combined with the barrier effect from the Cotentin Peninsula, see Figure 6.38 (c).
The intertidal zone – the coastal area affected by the tides – is exceptionally large: 200 km².
The bay is a UNESCO world heritage site for its aesthetic quality and its importance to the Christian tradition.
The Bay of Fundy
The official largest tidal range in the world is found in Nova Scotia’s Bay of Fundy. This is now disputed: with Ungava Bay, Nunavik claiming a 2 m higher tidal range.
With a length of 258 km, the Bay of Fundy has a wide opening into the Atlantic Ocean.
At its northern end, however, it splits into two narrow basins, Chignecto Bay and Minas Basin, see Figure 6.38 (b).
The period of free oscillation in the bay – the oscillation that occurs when a body is displaced and then released – is very nearly that of the tidal period.
The resulting constructive interference – along with the narrowing and shoaling of the bay to the north –
causes a buildup of tidal energy in the northern end of the bay.
In addition, the bay curves to the right, so the Coriolis effect in the northern Hemisphere adds to the extreme tidal range.
During maximum spring tide conditions, the tidal range at the mouth of the bay (where it opens to the ocean) is only about 2 meters.
However, the tidal range increases progressively from the mouth of the bay northward.
In the northern end of Minas Basin, the maximum spring tidal range is 17 meters, which leaves boats high and dry during low tide.
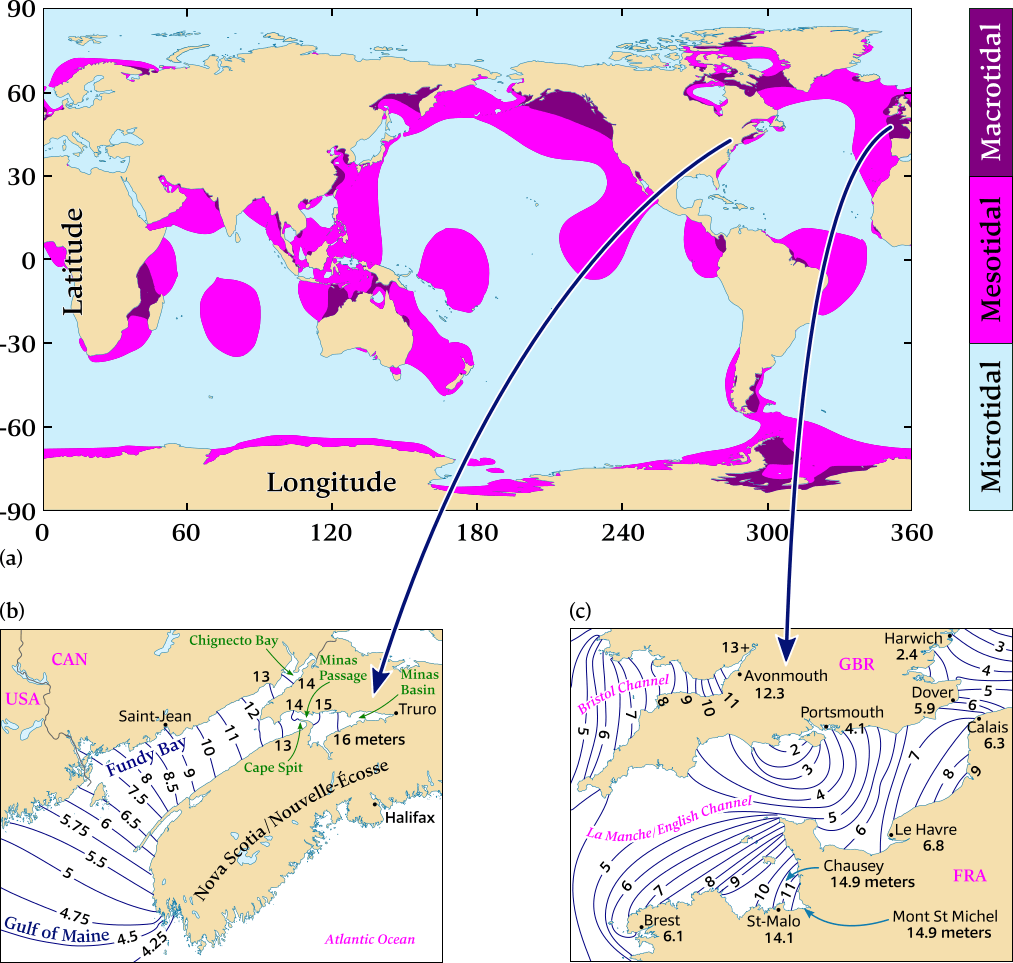
and the extreme tides of Fundy bay and Saint-Malo / Chausey.
(a) Microtidal: a tidal range lower than 2 metres. Mesotidal: a tidal range between 2 metres and 4 metres. Macrotidal: a tidal range higher than 4 metres.
(b) and (c) Extreme tides: the navy blue lines connect points with same spring tidal ranges.
(b) North of the Gulf of Maine (USA) is Fundy bay (Canada) which has the world record with a tidal range of over 16 meter.
(c) The France side of The English Channel / La Manche offers arguably the most impressive tides due to the immensity of this intertidal zone, famously at Saint-Malo and the Chausey archipelago in the Bay of Mont Saint-Michel.
Note that the ranges are far greater along the French coast than the English coast. This is due to the Coriolis force which directs the bulge to the right. Similarly, the water is curved up the Bristol Channel towards Avonmouth.
Mediterranean tides
Most people associate the Mediterranean with small tides. However, this is not to say there are no tides at all, as shown by this animation of measured Mediterranean tides.
Indeed, they generate a mean variation of about 40 centimeters, but atmospheric conditions often hide the rise and fall in sea level.
Headwinds or, more often, higher-than-normal atmospheric pressure attenuate the effect of these tides, sometimes making them virtually impossible to see.
However, for example, the Gulf of Gabes off the coast of Tunisia has a range of nearly two meters.
In other areas, such as the Adriatic and south of Sicily, tides are very small in the vicinity of amphidromic points where the tidal range is zero.
The Atlantic affects tides in the Strait of Gibraltar, but its influence soon declines further east.
Also see these sections of Greece:
Tidal curves show neap and spring ranges
Figure 6.39 shows examples of monthly tidal curves for various coastal locations.
Even though a tide at any particular location follows a single tidal pattern, it still may pass through stages of one or both of the other tidal patterns. Typically, however, the tidal pattern for a location remains the same throughout the year.
Also note that the tidal curves in Figure 6.39 clearly show the weekly alternating of the spring tide – neap tide cycle.
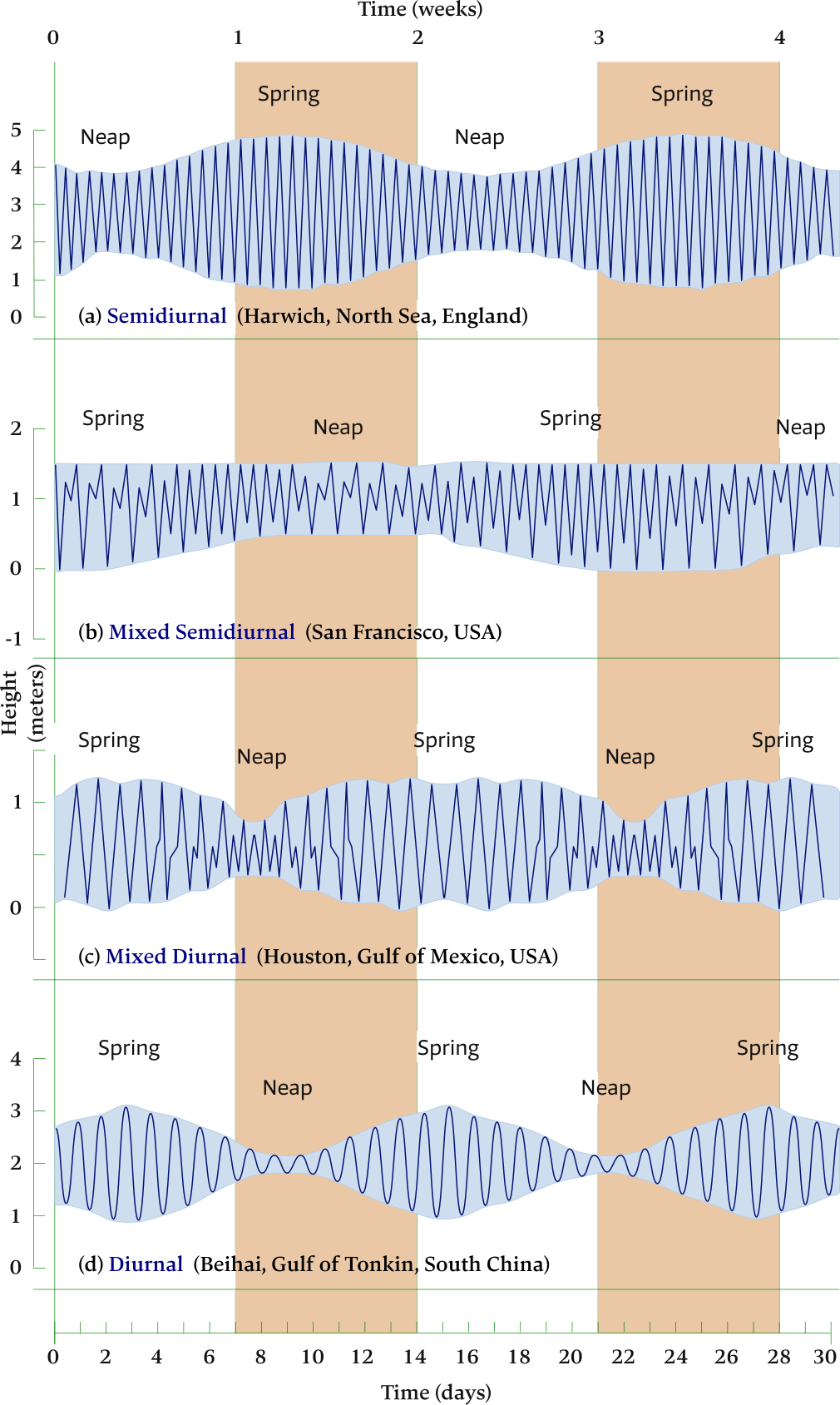

Horizontally the time is shown in weeks (indicated along the top) and days (indicated along the bottom).
(a) Harwich, north Sea, England – showing semidiurnal tidal pattern.
(b) San Francisco, USA – showing mixed semidiurnal tidal pattern.
(c) Houston, Gulf of Mexico, USA – showing mixed tidal pattern with strong diurnal tendencies.
(d) Beihai, Gulf of Tonkin, South China – showing diurnal tidal pattern.
Tidal bore
Mascarets or tidal bores are atypical waves. These are tidal waves that travel up rivers as illustrated in Figure 6.40. At the time of the tidal shift, a wave is formed and then moves up the stream against the direction of the current. The tidal bore is a well-known phenomenon in the Bristol Channel (Severn) as well as the Gironde, where it delights surfers and kayakers. This phenomenon can generate impressive waves: e.g. up to 6 meters high in the Qiantang river, travelling at 40 km/h.
German: “Gezeitenwelle”, Spanish: “macareo”, Dutch: “vloedbranding”, Italian: “mascheretto”.
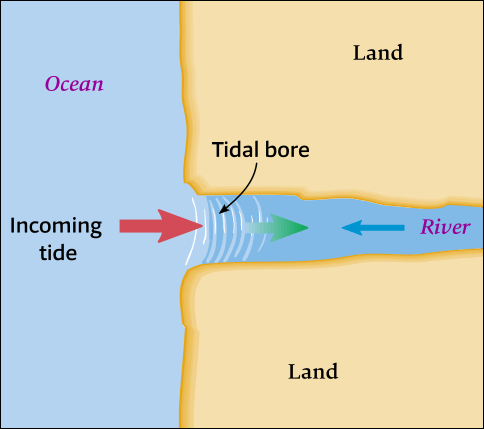
The leading edge of the incoming tide forms a wave (or waves) of water that travels upstream a river or narrow bay, reversing the direction of the river or bay's flow.
Etymology: “bore” derives (through Old English) from the Old Norse word 'bára', meaning “wave” or “swell”.
There are about 80 significant bores around the world.
Coastal tidal currents
The current that accompanies the slowly turning tide crest in a northern Hemisphere basin rotates counterclockwise ↺, producing a rotary current in the open portion of the basin. Friction increases in nearshore shoaling waters, so the rotary current changes to an alternating or reversing current that moves into and out of restricted passages along a coast.
The velocity of rotary currents in the open ocean is usually well below 1 km/h. Reversing currents, however, can reach velocities up to 44 km/h in restricted channels such as between islands of coastal waters.
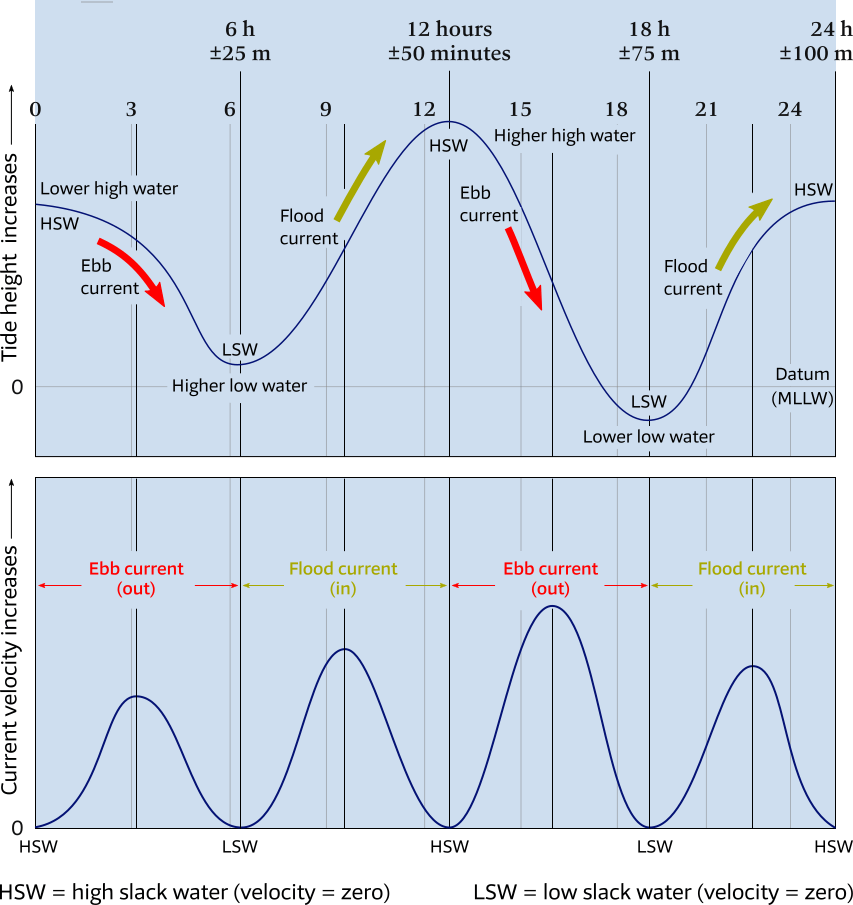
Top: Tidal curve for a bay, showing ebb currents are created by an outgoing low tide and flood currents are created by an incoming high tide.
No currents occur during either high slack water (HSW) or low slack water (LSW).
The datum “MLLW” stands for “mean lower low water”, which is the average of the lower of the two low tides that occur daily in a mixed tidal pattern.
Bottom: Corresponding chart showing velocity of ebb and flood currents.
Reversing currents also exist in the mouths of bays (and some rivers) due to the daily flow of tides. Figure 6.41 shows that a flood current is produced when water rushes into a bay (or river) with an incoming high tide. Conversely, an ebb current is produced when water drains out of a bay (or river) because a low tide is approaching. No currents occur for several minutes during either high slack water (which occurs at the peak of each high tide) or during low slack water (at the peak of each low tide).
Reversing currents in bays can sometimes create a navigation hazard for ships. On the other hand, the daily flow of these currents often keeps sediment from closing off the bay and replenishes the bay with seawater and ocean nutrients.
Further reading
- Historical background – Lunar Motion
- Major / minor Lunar standstills
- Tides and centrifugal force
- Coriolis and friction & Coriolis
- Lunar sidereal and synodic months [short animation]
- History of tidal science [Wikipedia]
- What physics teachers get wrong about tides! [Youtube – PBS SpaceTime]
- Visualization of Tidal Forces [Youtube – (non)-inertial (pseudo)-forces]
- Archaeoastronomy Database [Youtube – Astronomy concepts]
Overview
- Tide: For yachtpersons in particular, the tides are defined as the rise and fall of the surface of a body of water caused primarily by the differences in gravitational attraction of the Moon, and to a lesser extent the Sun, upon different parts of the Earth when the positions of the Moon and Sun change with respect to the Earth.
- Centripetal force: A net force that acts on an object to keep it moving along a circular path.
- Cotidal lines: Lines that radiate out from the amphidromic point.
- Gravitational force: A force that attracts any two objects with mass, measured from the centers of the objects.
- Lunar / Solar / Tidal bulge: The tidal bulge created on the sides of the Earth toward and away from the Moon and Sun.
- Zenith: The point of the Earth closest to the Moon, i.e. where the Moon is overhead.
- Nadir: The point of the Earth furthest from the Moon and opposite of the zenith.
- Resultant force: The mathematical difference of the forces acting on an object, resulting in the single force that represents the effects of all of the other forces acting on that object. Therefore, it is a net force, being equal to the sum of all forces applied to the object.
- Gradient: The rate at which a physical quantity increases or decreases relative to change in a given variable, especially distance.
- Syzygy : In astronomy this is a collinear configuration of three celestial bodies, from Greek Συζυγία “conjunction, yoked together”.
- Spring tide: The tidal effect of the Sun and the Moon acting in concert twice a lunar month, when the Sun, Earth and Moon are all in a straight line (Full Moon or New Moon) – syzygy. The range of tide is larger than average.
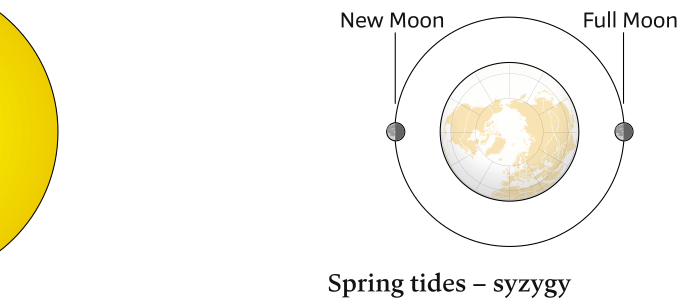
Note that in reality the Moon's orbit is elliptic, tidal bulges omitted.
- Neap tide: This opposite effect occurs when the Moon is at right angles to the Earth – Sun line (First or Last Quarter) – no syzygy. The range of tide is smaller than average.
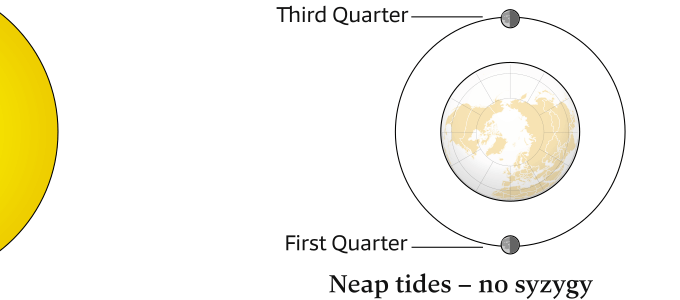
Note that in reality the Moon's orbit is elliptic, tidal bulges omitted.
- Range: The vertical difference between the high and low tide water levels during one tidal cycle.
- Tidal cycle: One high tide plus a successive low tide.
- Barycenter: In astronomy, the barycenter is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit.
- A top view of the solar system is the norm: northern hemisphere bias, and from this perspective both the Earth and the Moon are orbiting counterclockwise ↺.
- Tidal day or Lunar day: 24 hours and ±50 minutes. The Moon orbits the Earth every month, and the Earth rotates (in the same direction as the Moon's orbit) on its axis once every 24 hours.

(a) Semidiurnal, (semidaily) tides.
These are tides of the conventional form, with two tides, both of similar tidal range, within a lunarday: 24 hours 50 minutes; e.g. Savannah River Entrance, Georgia, U.S.A.
(b) Diurnal (daily) tides.
A single tide once within a lunar day; e.g. Pensacola, Alabama, U.S.A.
(c) Mixed semidiurnal tides.
Two tides of markedly different tidal range within a lunar day; e.g. Key West, Florida, U.S.A.
- Semidiurnal tide: The most common tidal pattern, featuring two highs and two lows each day, with minimal variation in the height of successive high or low waters.
- Diurnal tide: A tidal pattern with only a single high and a single low during each tidal day; successive high and low waters do not vary by a great deal, e.g. in the Gulf of Mexico, Java Sea and in the Tonkin Gulf.
- Mixed Tide or Mixed semidiurnal tide: This tidal pattern is characterized by a wide variation in heights of the successive high and low waters, and by longer tide cycles than those of the semidiurnal cycle, e.g. in the U.S. Pacific coast and many Pacific islands.
- Apsis, plural: Apsides: e.g. perigee, apogee, perihelion and aphelion.
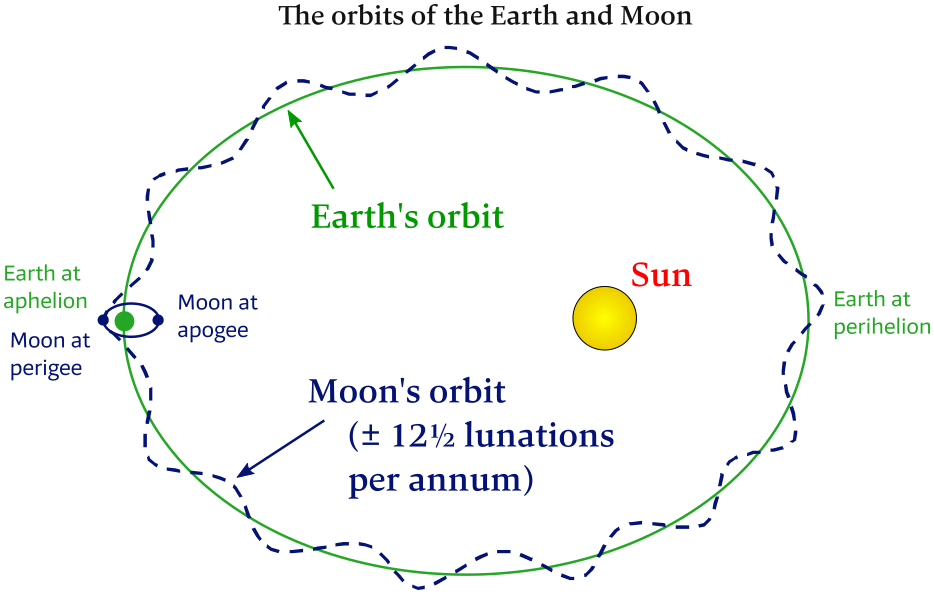
New Declination cycle: ± 27 days
Apsidal cycle: ± 27 days
Lunation cycle: ± 29 days
Earth – Moon barycenter left out, also see Figure 6.2.
- Declination: In astronomy this is the angle measured north or south of the celestial equator, much like the geographic “latitude”.
- Apogee: This is the point where the orbiting object (Moon) is farthest from it's parent (Earth).
Lunar apogee: 406,697 km. - Perigee: The point where the orbiting object is closest to its parent.
Lunar perigee: 356,410 km. - Line of apsides: A reference line passing through the orbital plane at perigee on one side and apogee on the other.
- Perihelion: The point in the elliptic orbit of a comet, planet, etc., where it is nearest to the Sun.
- Aphelion: The point in the elliptic orbit of a planet, comet, etc., where it is farthest from the Sun.
- Perigean spring tide: Colloquially known as a “king tide” and which typically occurs between 6 – 8 times each year; the New Moon or Full Moon coincides closely in time with the perigee of the Moon – the point when the Moon is closest to the Earth.
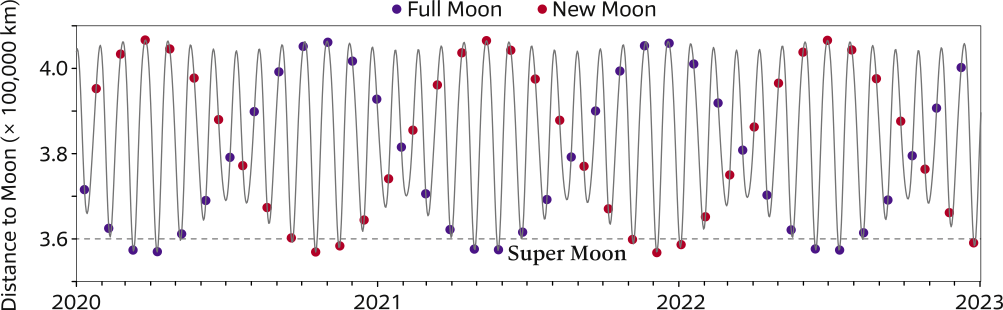
New Moon and Full Moon perigees.
- Apsidal precession: All orbits have two points where the orbiting body is either closest to, or furthest away from, the object (i.e. “parent”) it is orbiting. These points are called apsides, and the imaginary line between them is called the line of apsides. Apsidal precession is the gradual rotation of this line over time, which occurs in cycles of around 8.85 years for the Moon.
About every 4.45 years, the Sun is coincident with the line of apsides. Larger tidal ranges are experienced during these years, particularly around the time of the equinox when the Sun's declination is zero (which maximizes semidiurnal forces). - Ecliptic: The plane of the Earth’s orbit around the Sun.
- Orbital tilt of the Moon or inclination of the Moon's orbit: The Moon's orbital plane is inclined by about 5.1° with respect to the ecliptic.
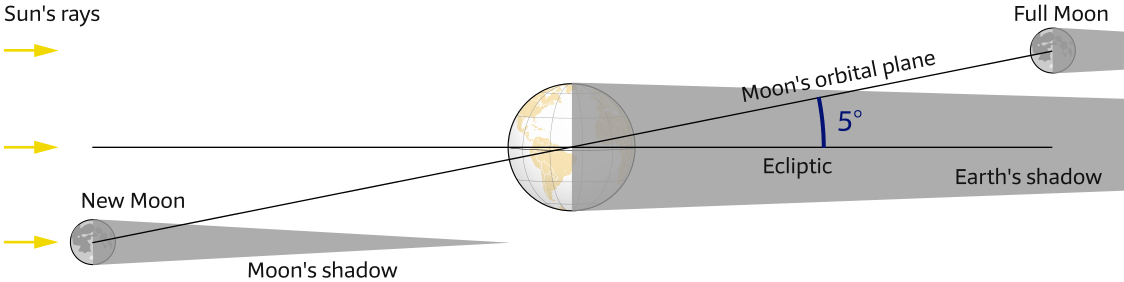
- Earth's axial tilt: The angle that the Earth's rotation axis makes with the ecliptic. The Earth is currently tilted 23.4° from this plane, and varies between 22.1° and 24.5° over time.
- Lunation is the 29 ½-day monthly tidal cycle.
Other synonyms are: lunar cycle, lunar month, and synodic month.
During the monthly tidal cycle, the phase of the Moon changes dramatically.
When the Moon is between Earth and the Sun, it cannot easily be seen at night, and it is called the New Moon.
When the Moon is on the side of Earth opposite the Sun, its entire disk is brightly visible, and it is called a Full Moon.
A Quarter Moon – a moon that is half lit and half dark as viewed from Earth – occurs when the Moon is at right angles to the Sun relative to Earth.
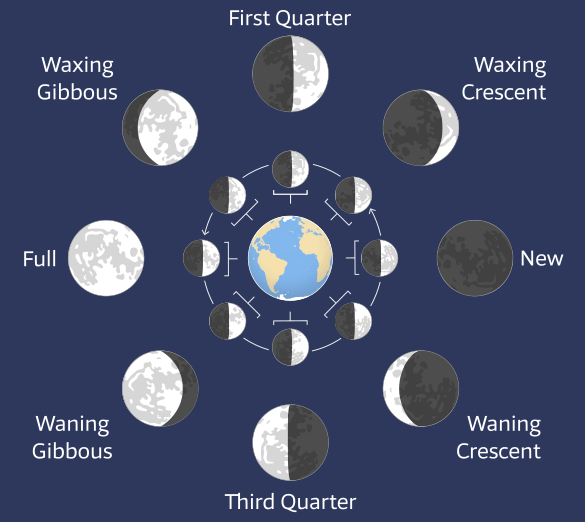
Inner ring with the Sunlight comes from the right.
Outer ring shows the phases as seen from the Earth.
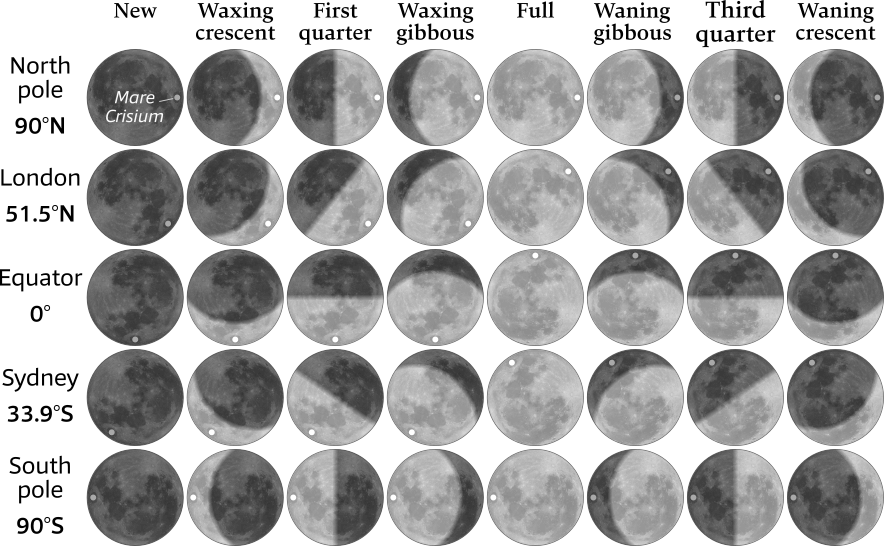
Mare Crisium meaning Sea of Dangers/Crises is an ancient asteroid impact plain. They were dubbed maria, Latin for 'seas', by early astronomers who mistook them for actual seas.
- Lunar nodes: There are two points, called nodes, at which the orbit of the Moon intersects the ecliptic.
- Ascending node, dragon's head, ☊︎, Caput Draconis: The ascending (or north) node is where the Moon moves into the northern ecliptic hemisphere.
- Descending node, dragon's tail, ☋︎, Cauda Draconis: The descending (or south) lunar node, the point at which the orbit of the Moon intersects the ecliptic entering the southern ecliptic hemisphere.
- Line of nodes: The line connecting the two lunar nodes of the Moon's orbit.
- Precession of the line of nodes or nodal precession: Because the orbital plane of the Moon precesses in space, the lunar nodes also precess around the ecliptic, completing one revolution – called a draconic or nodal period – in 18.6 years, i.e. the line of nodes of the Moon's orbit precesses 360° in this period of 18.6 years.
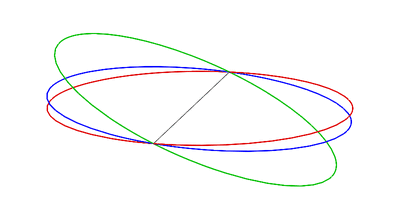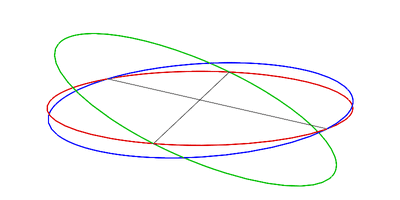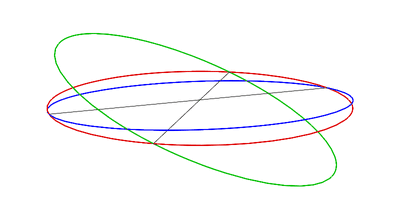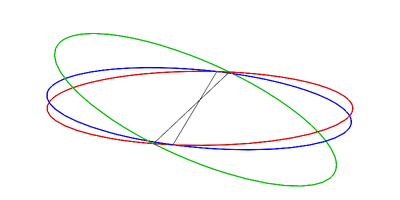
Interaction of the planes – animated. See animation online.
In this animation, the three planes are intersected with a sphere: the ecliptic is in red, the Earth's equator is in green, and the Moon's orbital plane is in blue.
The orbital plane of the Moon maintains a relatively constant inclination (tilt) to the ecliptic, which currently is about 5.1°.
The nodes precess along the ecliptic at a fairly constant rate.
The equator of the Earth is inclined about 23.4° to the ecliptic. - Draconic month: This period is also known as Nodical month, Draconitic, Nodal month [Wiki] or Draconic period, which is 27.21 days (i.e. 27 days 5 hours 5 minutes), and is the time between the Moon’s passages through the same node, or intersection of its orbit with the ecliptic.
- Sidereal time: Time as measured by the apparent motion about the Earth of the distant, so-called fixed, stars, as distinguished from solar time, which corresponds to the apparent motion of the Sun.
To be specific, in the time it takes the Earth to spin once about its axis, it also moves along its orbit by over 2.5 million kilometers. Because the Earth has moved, the Sun will not appear in the same part of the sky at the end of that rotation. To end up facing the Sun again, the Earth has to rotate for another four minutes. In other words, a solar day is how long it takes Earth to rotate once – and then some. A sidereal day – 23 hours 56 minutes and 4.1 seconds – is the amount of time needed to complete one rotation.
Astronomers rely on sidereal time keeping because any given star will transit the same meridian at the same sidereal time throughout the year.
Sidereal time may be defined for any place on the Earth, but in the international system used by astronomers each sidereal day begins at the instant the vernal equinox transits the prime meridian. - Sidereal month: The time it takes for the Moon to make one full orbit of the Earth relative to the stars.
One Sidereal month = 27.3 days
= 27 days 7 hours 43 minutes.
From Latin “sidereus”, from sider-, sidus star, constellation. Hence, “sidereal”: relating to, or expressed in relation to stars or constellations, see sidereal period / month [Wiki]. - Synodic month: A synodic day is like the solar day on Earth, and a synodic month is defined as the time required to go through all of the lunar phases.
- This is different from a sidereal month because the Earth – Moon system is orbiting the Sun.
- At the end of a sidereal month the Earth has moved around the Sun and the Moon has further to go until it reaches the New phase.
- A synodic month is therefore longer than a sidereal month.
One synodic month = 29.53 days.Because of the motion of the Moon around the Earth,
it rises about 50 minutes later each day.
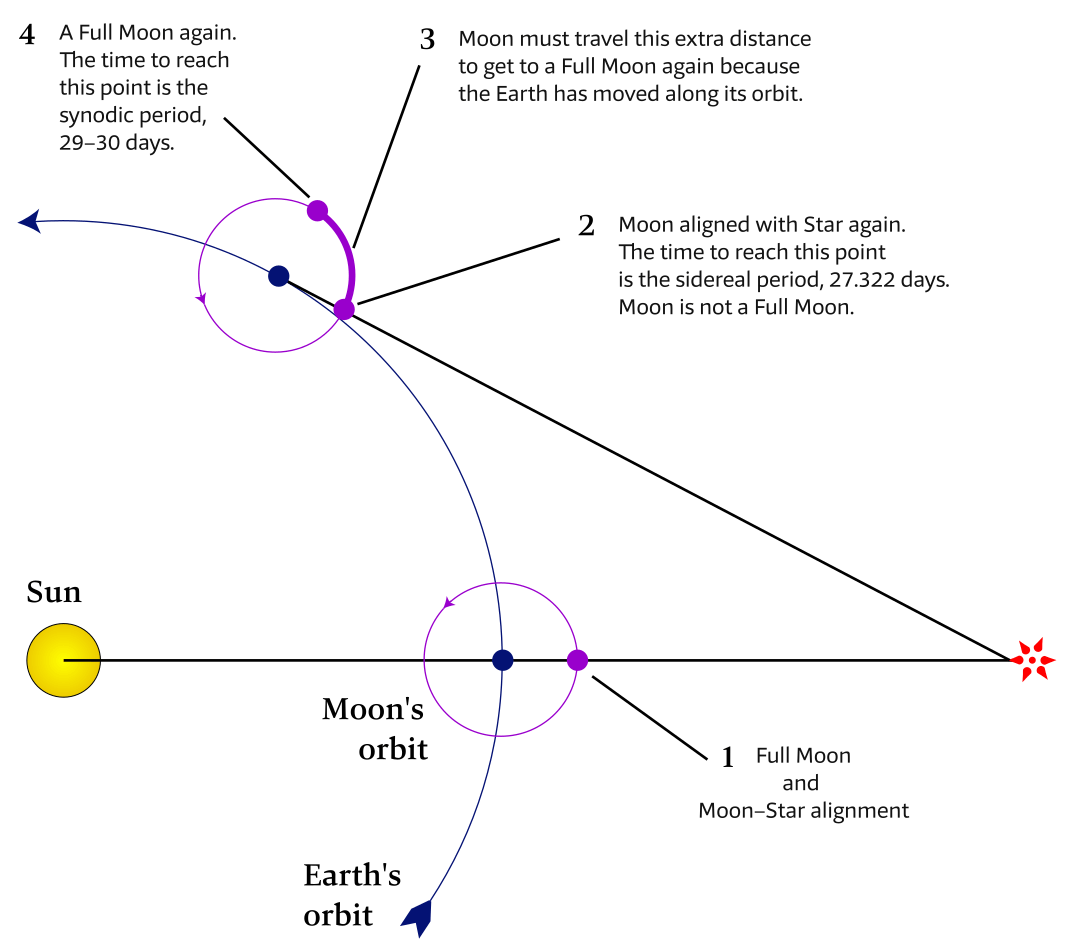
See the next chapter…
- Course overview: goals and introduction
- Positions: latitude, longitude, nautical mile, scale, knots
- Nautical chart: coordinates, positions, courses, chart symbols, projections
- Compass: variation, deviation, true • magnetic • compass courses
- Plotting and piloting: LOPs, (running) fix, dead reckoning, leeway, CTS, CTW, COG
- Advanced piloting: double angle on the bow • four point • special angle fix, distance of horizon, dipping range, vertical sextant angle, radians, estimation of distances
- Astronomical origin of tides: diurnal, semi-diurnal, sysygy, spring, neap, axial tilt Earth, apsidal • nodal precession, declination Moon and Sun, elliptical orbits, lunar nodes
- Tides: tidal height prediction, chart datums, tidal curves, secondary ports
- Tidal streams and currents: diamonds, Course to Steer, Estimated Position
- Aids to navigation: buoys, leading lights, ranges, characteristics, visibility
- Lights and shapes: vessels sailing, anchoring, towing, fishing, NUC, RAM, dredging
Also you can download the exercises + answers PDF ![]()